V předešlém článku jsme si řekli o dekompozici součinitele zeslabení µ(r, E) pro materiál voxelu na dva různé součinitele zeslabení pro předem známé materiály, většinou vodu a jod. Každý ze dvou součinitelů zeslabení f_1(E) a f_2(E) v rovnici (1) je lineární kombinací součinitelů zeslabení pro dvě dominantní interakce, pro fotoefekt a Comptonův rozptyl. Rayleighův rozptyl zde zanedbáme. V tomto článku si řekneme více o závislostech koeficientů f_1(E) a f_2(E).

(1)

Označme si koeficient f_i(E) pro libovolný materiál jako µ_i(E). Rovnici (1) pak lze přepsat následovně:

(2)

Pro koeficient µ_i(E), ať pro vodu nebo jod nebo jiný materiál, platí:

(3)

kde µ_f(E) je součinitel zeslabení pro fotoefekt, µ_C(E) je součinitel zeslabení pro Comptonův rozptyl. Jak víme již z interakcí pro fotoefekt a Comptonův rozptyl, Comptonův rozptyl závisí na energii E a elektronové hustotě ρ_e, která je úměrná hustotě materiálu ρ. Fotoefekt silně závisí na protonovém čísle materiálu Z, energii E a méně na hustotě materiálu ρ. Součinitele zeslabení µ_f(E) a µ_C(E) lze pak napsat následovně:

(4)

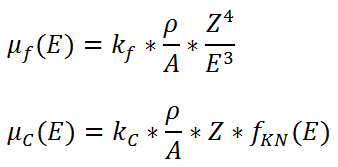
kde k_f a k_C jsou empirické konstanty, Z je protonové číslo materiálu, A je hmotnostní číslo materiálu, f_KN je koeficient z Klein-Nishinovy formule, který vykazuje závislosti podobnou E^(-1), ρ*(Z/A) odpovídá elektronové hustotě ρ_e. Poměr Z/A je téměř konstantní (≈0,5) pro všechny prvky s výjimkou vodíku a těžkých prvků, které se v lidském těle nevyskytují.

Pro materiály s nízkým Z, myšlena voda a vodě-podobné, např. měkké tkáně, je lineární součinitel zeslabení µ(E) převážně určen součinitelem pro Comptonův rozptyl µ_C(E), který je při CT energiích v měkké tkáni zastoupen ve větší míře než fotoefekt. U materiálů s vyšším Z, tedy v kostech a kontrastních látkách, je lineární součinitel zeslabení µ(E) převážně určen součinitelem pro fotoefekt µ_f(E), který je zastoupen ve větší míře. Díky těmto rozdílným zastoupením interakcí lze v obraze rozeznat různé materiály.

Z první rovnice (4) vidíme, že zastoupení fotoefektu klesá s rostoucí energií přibližně se třetí mocninou, tj. ~1/E^3. Zastoupení Comptonova rozptylu také klesá s rostoucí energií, tj. je úměrná ~1/E. Rovnici (3) lze použitím rovnic (4) pak přepsat následovně:

(5)kde koeficienty f(r) a c(r) jsou koeficienty specifické pro každý materiál a jsou závislé na hustotě ρ, protonovém čísle Z a hmotnostním čísle A materiálu obsaženém v pixelu r.

Mějme CT spektrum produkované při napětí 120 kV, jehož efektivní energie je cca 65 keV. Budeme-li se snažit odlišit kost a jodovou kontrastní látku, velmi pravděpodobně se nám to nepodaří. CT číslo u obou těchto materiálů se bude pohybovat kolem 1000 HU. Získáme-li však data při nižších energiích, např. při napětí 80 kV (efektivní energie cca 55 keV), kdy je rozdíl mezi zeslabením kosti a jodové kontrastní látky větší, umožní nám to lépe rozlišit jednotlivé materiály, protože i CT čísla budou rozdílnější. Data získána při nižší energii jsou kombinována s daty získanými při vyšší energii, typicky při 140 kV, případně 150 kV.

Použitá literatura:
Johnson TRC. Dual energy CT in clinical practice. Heidelberg: Springer, c2011. Medical radiology. ISBN 3642017401
Heismann B, Schmidt B, Flohr T. Spectral computed tomography. Washington: SPIE Press, 2012. ISBN 978-0-8194-9257-9
Russo P. Handbook of X-ray imaging. Physics and technology. Series in Medical Physics and Biomedical Engineering. CRC Press, 2018. ISBN 978-1-4987-4152-1