U rekonstrukce CT obrazu je základním úkolem zjistit hodnoty zeslabení v každém pixelu (neboli hodnoty každého pixelu matice), na základě nichž pak lze určit materiál v daném pixelu (voxelu). Využívá se několika typů rekonstrukcí, základní je rekonstrukce pomocí zpětné projekce, porkočilejší je pak iterativní rekonstrukce.

Nejprve si řekneme, jak probíhá rekonstrukce CT obrazu pomocí zpětné projekce. Nechť má původní matice 3×3 následující hodnoty jednotlivých pixelů:

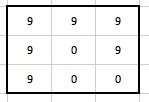
Při rekonstrukce však jednotlivé hodnoty pixelů neznáme, cílem rekonstrukce je tyto hodnoty zjistit. Rekonstrukce vychází ze známých profilů zeslabení v různých projekcích. Nechť máme v naší zjednodušené situaci projekce BP1 (červená), BP2 (modrá) a BP3 (zelená), graficky znázorněné následovně (hodnoty pixelů matice jsou pouze šedivé, neboť je neznáme):

Profily zeslabení pro jednotlivé projekce jsou následující:

BP1: 

BP2: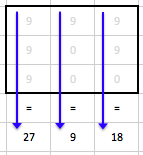

BP3: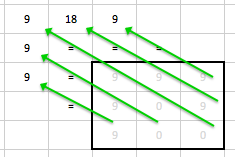

Hodnoty v jednotlivých projekcích budeme rozdělovat rovnoměrně do všech pixelů, kterými prochází „paprsek“ dané projekce. Celkem máme 3 projekce, proto hodnoty hned zpočátku vydělíme číslem 3. Začneme u projekce BP1, řádku 1:

Nejprve hodnotu 27 vydělíme 3, dostaneme 9. Tuto hodnotu rozdělíme rovnoměrně do všech tří pixelů (prvků) prvního řádku. Do každého pixelu tedy vložíme hodnotu 3. Stejně tak pro druhý řádek, hodnotu 18 vydělíme 3 (máme 3 projekce) a pak znovu 3 (hodnotu rozdělíme do 3 pixelů). Dostaneme 2. Tuto hodnotu vložíme do každého pixelu druhého řádku. Podobně pro třetí řádek matice: Hodnotu 9 vydělíme 3, tj. máme 3. Tuto hodnotu rozdělíme rovnoměrně do každého prvku třetího řádku, takže do každého prvku vložíme hodnotu 1. Námi získaná matice odvozená z BP1 vypadá následovně:

Pro BP2 vypadá odvozená matice následovně:

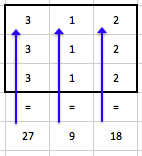
Pro BP3 vypadá odvozená matice následovně:

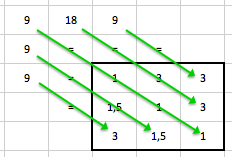
Nyní všechny tři odvozené matice sečteme. Dostáváme matici s následujícími hodnotami:

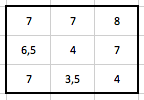
Toto je pak výsledná zrekonstruovaná matice, která předstauje CT obraz v daném řezu. Porovnáme-li hodnoty s hodnotami původní matice, zjistíme, že jsou mírně odlišné. Hodnoty jsou jakoby „vyhlazené, rozdíl mezi vysokými a nízkými hodnotami vedlejších pixelů je menší. Např. prostřední hodnota a hodnota nad ní: původně 0 a 9 (rozdíl 9), v nové matici 4 a 7 (rozdíl 3). Ve výsledném obrazu se tento efekt projeví rozmazáním (blurring) a šumem. Obraz lze zlepšit filtrací dat, ale o tom až jindy…

Nyní k iterativní rekonstrukci. Iterativní rekonstrukce vychází buď z již zrekonstruované matice použitím zpětné projekce, nebo zjednodušeně z nulové matice (výchozí matice může být v podstatě jakákoliv). Použijme jako počáteční nulovou matici:

Mimoto známe i profily zeslabení pro každou projekci, pro náš zjednodušený případ pro projekce BP1, BP2 a BP3:

Sečteme-li hodnoty v prvním řádku původní (nulové) matice, dostáváme součet 0. Potřebujeme dostat součet 27. Číslo 27 rozdělíme rovnoměrně do 3 pixelů, do každého přidáme hodnotu 9. Podobně pro druhý řádek, hodnotu 18 rozdělíme do 3 pixelů, tedy do každého 6. Podobně pro třetí řádek. Matice po dosazení hodnot z BP1 vypadá následovně:

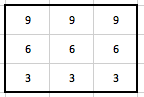
Pro BP2 již bereme matici, která vznikla použitím BP1. Z projekce BP2 plyne, že součet pixelů v prvním sloupci je roven 27. Z matice odvozené v předešlém kroku použitím BP1 již máme součet v prvním sloupci roven 18. Rozdíl je roven 27-18=9. Takže hodnotu 9 rozdělíme rovnoměrně na tři hodnoty, které přičteme ke stávajícím hodnotám v matici. Tedy 9/3=3, proto do každého pixelu prvního sloupce přičtu 3.

Podle profilu zeslabení je součet v druhém sloupci roven 9. V matici odvozené z BP1 je součet v druhém sloupci roven 18. Rozdíl 9-18=-9. Tedy hodnoty -9 rozdělím rovnoměrně do všech tří pixelů druhého sloupce, ke každému pixelu přičtu hodnotu -3. Podobně pro třetí sloupec (rozdíl je roven 0, proto se pixely posledního sloupce nemění). Výsledná matice je následující:

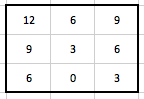
Zbývá nám projekce BP3. Součet pro jednotlivé paprsky je roven 9, 9, 9, 18, 9, jak ukazuje následující grafické znázornění:

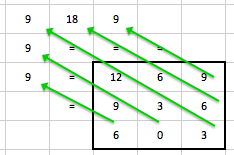
Stejným způsobem, jako pro BP1 a BP2 zkorigujeme hodnoty v jednotlivých paprscích BP3. Dostáváme:

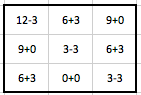
Výsledná matice je rovna:

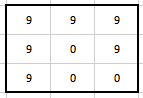
Tato matice odpovídá i původní matici, jejíž hodnoty pixelů jsme hledali. Zde je zřejmé, že iterativní rekonstrukci poskytuje lepší výsledek než zpětná projekce, ale pro její praktické použití je nutné mít dostatečnou výpočetní kapacitu. Kdybychom vycházeli místo nulové matice z matice, která nám vyšla při výpočtu zpětnou projekcí, byla by po prvním kole iterace výsledná matice následující:

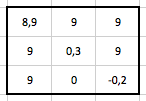
Aplikujeme-li další kolo iterace, výsledná matice bude více a více podobná původní matici. Obecně je iterativní rekonstrukce výpočetně náročnější (jedná se o rekonstrukci matice 512×512 v několika řezech, nikoliv pouze 3×3 v jednom řezu) než rekonstrukce použitím zpětné projekce, což je i jejím největším limitujícím faktorem.