Diagnostické referenční úrovně pro CT pro různé indikace

Napsat komentář

V České republice jsou národní diagnostické referenční úrovně (DRÚ) pro CT vyšetření stanoveny pro několik anatomických oblastí, viz Příloha č. 22 vyhlášky 422/2016 Sb., o radiační ochraně a zabezpečení radionuklidového zdroje.

Obr. 1: DRÚ pro CT (Příloha č. 22 vyhlášky 422/2016)

Při pohledu na stanovené národní DRÚ je zřejmé, že se jedná o anatomical-based DRÚ neboli DRÚ založené pouze na anatomické oblasti. Nevýhodou těchto DRÚ je to, že nezohledňují klinickou indikaci, tedy důvod, proč byl pacient vyšetřen. Např. u CT vyšetření břicha není zřejmé, šlo-li o zobrazení z důvodu metastází v játrech nebo se hledaly ledvinové kameny. Zrovna tyto dvě indikace vyžadují velmi rozdílnou kvalitu CT obrazu, tedy i dávku pacientovi. Pro nalezení ledvinových kamenů, které jsou hodně kontrastní, stačí podstatně nižší dávka, než je potřeba pro hledání metastází v játrech, kdy se jedná o hledání nízkokontrastních lézí. V takovém případě je potřeba snížit šum, aby léze byly viditelné, tedy vyšetření vyžaduje vyšší dávku pacientovi. Současně se vyšetření jater provádí vícefázově, což opět zvyšuje dávku v porovnání s vyšetřením z důvodu ledvinových kamenů.

DRÚ stanovené na základě klinické indikace se označují jako clinical-based DRÚ. Přehled možných indikací pro CT vyšetření a tedy pro stanovení clinical-based DRÚ je uveden na obr. 2.

Obr. 2: Indikace pro stanovení clinical-based DRÚ pro CT vyšetření (převzato z Diagnostic Reference Levels based on clinical indications in computed tomography: a literature review – PMC (nih.gov))

Národní, ale i místní, DRÚ stanovené na základě indikací dávají mnohem větší smysl a stále více zemí se k tomuto přístupu uchyluje. Nedávno byly revidovány hodnoty DRL v UK, které jsou již clinical-based. Současně vyšla publikace, která shrnuje informace o sběru dat na základě dotazníků, který vyplnila pracoviště v UK a zahrnula do nich informace z více než 750 tis. CT vyšetření. V publikaci je uvedena spousta důležitých informací, např. u kolika vyšetření je používána automatická modulace proudu nebo iterativní rekonstrukce. Tím se samozřejmě získá více informací potřebných k „ověření“ toho, zda je DRÚ nebo nějaká místní průměrná dávka dostatečně nízká. Mám tím na mysli to, že budu-li mít relativně nový CT, u kterého využívám pokročilou iterativní rekonstrukci, tak by průměrné dávky stanovené z tohoto skeneru měly být nižší než průměrné dávky stanovené na starším CT skeneru pro tutéž indikaci.

Stanovením clinical-based DRÚ se zabýval také evropský projekt EUCLID (European Study on Clinical DRLs), jehož výstupem jsou clinical-based DRÚ. Současně vyšlo i mnoho dalších studií na toto téma, tady aspoň malý přehled.

  • Paulo G, Damilakis J, Tsapaki V, et al. Diagnostic Reference Levels based on clinical indications in computed tomography: a literature review. Insights Imaging. 2020;11(1):96. Published 2020 Aug 17. doi:10.1186/s13244-020-00899-y
  • Tsapaki V, Damilakis J, Paulo G, et al. CT diagnostic reference levels based on clinical indications: results of a large-scale European survey. Eur Radiol. 2021;31(7):4459-4469. doi:10.1007/s00330-020-07652-5
  • Bos D, Yu S, Luong J, et al. Diagnostic reference levels and median doses for common clinical indications of CT: findings from an international registry. Eur Radiol. 2022;32(3):1971-1982. doi:10.1007/s00330-021-08266-1
  • National Diagnostic Reference Levels (NDRLs) from 14 June 2022 – GOV.UK (www.gov.uk)
  • AlNaemi H, Tsapaki V, Omar AJ, et al. Towards establishment of diagnostic reference levels based on clinical indication in the state of Qatar. Eur J Radiol Open. 2020;7:100282. Published 2020 Oct 28. doi:10.1016/j.ejro.2020.100282

Webinář IOMP-ICRP – Jsou dávky pod 100 mGy rizikové?

Napsat komentář

Dne 20.4.2022 se uskuteční webinář na velmi zajímavé téma „Are radiation risks below 100 mGy for example through recurrent CT procedures of real concern for radiological protection?“. Více zde: IOMP-ICRP Webinar: Are radiation risks below 100 mGy for example through recurrent CT procedures of real concern for radiological protection? , April 20, 2022 – International Organization for Medical Physics

Novinky na poli CT skenerů

Napsat komentář

Na RSNA 2021 představilo mnoho CT výrobců své novinky. Na trhu jsou nabízeny v současné době CT skenery s počtem řezů 64 až 640, některé s již photon-couting detektory, které umožňují redukovat šum a zlepšit prostorové rozlišení.

Fujifilm představilo na veletrhu svoji vlajkovou loď – CT skener SCENARIA View, včetně posledních pokroků pro redukci pohybových artefaktů při zobrazování srdce (Cardio StillShot, čeká na schválení FDA), které se objevují u pacientů s rychlým a nepravidelným srdečním rytmem. SCENARIA View již zahrnuje také software pro redukci artefaktů vznikajících v případě, kdy jsou paže podél těla pacienta. Samozřejmostí je také pokročilá redukce kovových artefaktů. SCENARIA View je CT skener s nejkratší dobou rotace 0,35 s, s nejmenší tloušťkou řezu 0,625 mm, se 64 řadami detektorů, s otvorem gantry 80 cm. Další technické detaily je možné získat zde: SCENARIA VIEW | Fujifilm Healthcare.

GE Healthcare představilo novou platformu u CT skeneru Revolution Apex, kdy je možné přímo na místě provést upgrade detektorů ze 40 mm na 80 mm nebo na 160 mm, aniž by musela proběhnout výměna gantry. Dále GE ukázalo také svou snahu na poli umělé inteligence (AI), která by měla pomoci vyhořelým radiologům s popisy nyní, ale i s těmi s použitím photon-counting detektorů, kdy se bude jednat o lepší vizualizaci drobných detailů a lepší charakteristiku tkání, včetně kvantifikace. Výrobce představil také nástroj pro zlepšení workflow na pracovišti, kdy jsou téměř všechny kroky podporovány AI, např. automatická centrace pacienta, automatická volba vyšetřovacího protokolu, což vede k lepší kvalitě obrazu za nižší dávky.

Philips představil novou platformu CT Smart Workflow, která podobně, jako bylo zmíněno výše, vede k lepší péči zaměřené přímo na konkrétního pacienta. Dalším pokrokem je integrace spektrálního CT Spectral CT7500 do angiografického systému Azurion, což umožňuje lepší charakteristiku a vizualizaci tkání. To může vést k nižší míře následných follow-upů pacienta po výkonu. Více zde: Philips Angio Spectral CT – News | Philips.

Obr. 1: Angiografický systém s integrovaným spektrálním CT (Philips Angio Spectral CT – News | Philips)

Siemens představil první photon-counting CT skener NAEOTOM Alpha, který má již také schválení FDA. FDA označilo využití photon-counting detektorů jako hlavní pokrok v CT zobrazování za poslední desetiletí. NAEOTOM Alpha je skener se dvěma zdroji záření a se dvěmi sadami detektorů, které umožňují získat spektrální informace o materiálu. Detektory také umožňují získat lepší prostorové rozlišení, redukovat kalcifkace a artefakty z toho plynoucí a v neposlední řadě vede použití detektorů k eliminaci elektronického šumu. Díky tomu je možné použít menší detekční elementy, a tím získat lepší prostorové rozlišení bez potřeby vyšší dávky. Výrobce představil také nejpokročilejšího zástupce z řady jednozdrojových CT skenerů s energii integrujícím detektorem – SOMATOM X.ceed CT. Tento skener je vhodný pro bariatrické pacienty, čemuž je uzpůsoben i otvor gantry – 82 cm. Součástí je také podpora workflow na pracovišti pomocí pěti tabletů k ovládání CT skeneru. Doba rotace je 0,25 s, což umožňuje i zobrazení srdce.

United Imaging Healthcare Solutions představili uCT ATLAS. Tento CT skener vyniká spojením AI a iterativní rekonstrukce, což umožňuje zlepšit dávku, šum, rozlišení a také vizuální dojem z CT obrazu. Skener automaticky zjistí pomocí 3D kamery habitus a polohu pacienta, není tedy potřeba, aby radiologičtí asistenti korigovali centraci pacienta manuálně. Za zmínku stojí to, že všechny pokročilé nástroje jsou součástí základní verze CT skeneru, není je potřeba dokupovat extra. Více informací zde: uCT® ATLAS | United Imaging (united-imaging.com).

Jaký byl letošní kongres RSNA?

Napsat komentář

Letošní kongres RSNA 2021 se nesl v duchu deep learning a CT s photon-counting detektory. Tedy vzato z fyzikálního pohledu. Tu a tam se objevila i přednáška z oblasti jiné, např. intervenční, ale největší část přednášek se zabývala právě dvěma zmíněnými tématy.

Firma Siemens oficiálně představila první CT s photon-counting detektory (volně lze přeložit jako detektory čítající jednotlivé fotony), firma Canon uvedla alespoň příspěvek s tím, kam se v oblasti photon-counting detektorů u CT dostali oni.

CT s photon-counting detektory (zde již mluvíme o spektrálním zobrazení) by měly jednoznačně přispět ke zlepšení kvality CT obrazů snížením šumu, lepším prostorovým rozlišením a přesností v jodových obrazech, umožňující kvantitativní hodnocení. A v neposlední řadě by měly umožnit také snížení radiační zátěže pacientů, protože je vhodným prahováním možné odstranit elektronický šum, tedy i potřebný počet fotonů a tedy snížit radiační zátěž.

Porovnejme si nyní technologii klasických energy-integrating detektorů (EID, detektory integrující energii přes celý detekční element) s photon-counting detektory (PCD, detektory čítajícími jednotlivé fotony). Grafické znázornění technologie EID a PCD je na obr. 1.

Obr. 1: Technologie EID a PCD [1]

EID využívá scintilačního materiálu, ve kterém dochází po absorpci rtg fotonu ke vzniku fotonů viditelného světla (záblesků), které dopadají na fotodiodu, ve které dochází ke vzniku signálu. Jedná se o dvoustupňový proces. U PCD se využívá polovodičový detektor, ve kterém po absorpci rtg fotonu vznikají páry elektronů a děr, které putují přímo k elektrodám, kde dochází ke vzniku signálu. Detekční elementy EID jsou obvykle větší než detekční elementy PCD, což společně s polovodičovým detektorem umožňuje získat lepší prostorové rozlišení. V ultra vysokém rozlišení je možné při použití PCD získat rozlišení až 40 lp/cm (u Naeotom Alpha, Siemens). Např. u prototypu firmy Canon je to prozatím pouze 8 lp/cm, ale pracují dále právě na ultra vysokém rozlišení. Ukázka CT obrazů z CT s EID (Flash, Force) a z CT s PCD a PCD s UHR (ultra vysoké rozlišení) je uvedena na obr. 2.

Obr. 2: Prostorové rozlišení dvou CT skenerů s EID (Flash, Force) a z CT skeneru s PCD [2] (A – axiální řez, B – sagitální řez)

Bylo zajímavé nahlédnout pod pokličku toho, co se děje při CT rekonstrukci, která využívá umělou inteligenci (nejčastěji deep learning, DL), kde všude v procesu zpracování obrazu lze DL použít. Lze to aplikovat např. na raw projection data (hrubá data), kdy můžeme pomocí toho provést korekci na rozptyl, tvrdnutí svazku a kovové artefakty. Nebo to můžeme využít o krok dále, při zpětné projekci, např. ke korekci podvzorkovaných dat nebo opět k redukci kovových artefaktů. Lze to však použít ještě v dalším kroku, kterým je čtení obrazu radiology. Prozatím jsou na trhu dostupné systémy s integrovanou DL rekonstrukcí pro dva výrobce – TrueFidelity od firmy GE a AiCE od firmy Canon.

Na kongresu také v nejedné přednášce zaznělo, že umělou inteligenci lze aplikovat hlavně pro korekci šumu u nízkodávkových vyšetření, ale na druhé straně zazněly také nevýhody s tím spojené, kterými je ztráta některých nízkokontrastních lézí nebo také trochu „umělý“ vzhled CT obrazů pro radiology, pro které je pocitově obraz někdy až moc hladký, takže působí uměle.

Spousta přednášek se zabývala již zmíněnými CT s photon-counting detektory, ale zajímavé byly také přednášky, které se zabývaly použitím photon-counting detektorů i mimo oblasti CT, např. při 3D rotační angiografii získané na angiografickém systému.

Kongres letos kvůli pandemii covidu nenavštívilo zdaleka tolik zájemců, ale i tak se jednalo, alespoň pro mě, o velmi přínosný kongres, na kterém šel vidět posun právě k DL a k CT s PCD. To je ve zkratce vše, uvidíme, čeho se v budoucnu dočkáme v klinickém použití a co naopak bude slepá větev.

Použitá literatura
[1] Flohr, T. Performance evaluation of  a dual source CT with two photon couting detectors. RSNA 2021.
[2] Photon-counting CT: Technical Principles and Clinical Prospects – PubMed (nih.gov)

Odkud a kam se vyvinulo rtg zobrazení

Napsat komentář

7. listopadu se slaví International Day of Medical Physics. Při této příležitosti jsem narazila na krásný obrázek ilustrující, jak se vyvinulo zobrazení s použitím rtg záření. Myslím, že k tomu není potřeba víc dodávat.

Převzato z https://www.linkedin.com/posts/ctisus_happy-international-day-of-radiology-activity-6863491912272236545-wN6i.

Skiagrafie použitím dvou energií

Napsat komentář

Vezmeme-li klasické skiagrafické zobrazení, jedná se o sumaci 3D objektu do 2D obrazu, přičemž se sumuje plicní tkáň, měkká tkáň i kosti. Skiagrafické zobrazení použitím dvou energií je typ zobrazení, který využívá dvou energií k tomu, aby byla z radiogramu odstraněna nepotřebná anatomie, např. kosti při popisu radiogramu srdce a plic. Anebo naopak, aby byly odstraněny měkké tkáně a zůstaly pouze kosti, případně jiné více zeslabující materiály. Odečtením některých nepotřebných anatomií, např. kostí, se může v radiogramu zvýraznit informace, která by na běžném radiogramu byla stěží nebo hůře rozpoznatelná a radiolog ji při popisu může opomenout.

Nyní k principu zobrazení s použitím dvou energií. Pro odstranění nežádoucí anatomie z obrázku se využívá odečtení dvou vážených radiogramů, které byly pořízeny při různých energiích. Mějme jeden radiogram získaný při napětí 60 kV (efektivní energie cca 40 keV) a druhý při napětí 120 kV (efektivní energie cca 60 keV). Hmotnostní součinitele zeslabení pro tyto dva svazky jsou znázorněny na obr. 1, na kterém jsou součinitele pro čtyři materiály. Pro kost a hliník, protože kost se často simuluje hliníkem, a pro vodu a plexisklo, protože voda, a tedy i měkká tkáň, se často simuluje plexisklem.

Obr. 1: Hmotnostní součinitele zeslabení – zeleně je označena efektivní energie cca 60 kV rtg svazku, červeně efektivní energie cca 120 kV rtg svazku (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

Radiogramy pořízené použitím rtg svazků s různým napětím jsou uvedeny na obr. 2. Pod každým radiogramem je také znázorněno relativní zeslabení měkké tkáně a kosti. Z hodnot relativního zeslabení je vidět, že při nižší energii má kost podstatně vyšší zeslabení a tedy i kontrast v obraze než při použití vyššího napětí, kdy zeslabení měkké tkáně a kosti není tak významně odlišné.

Obr. 2: Radiogram pořízený při 60 kV (vlevo) a 120 kV (vpravo), relativní zeslabení měkké tkáně a kosti a tomu odpovídající kontrast jsou znázorněny pod oběma radiogramy (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

Nyní si ukážeme, jak funguje vážení a následná subtrakce (odečtení) obrazů. Z obr. 2 víme, že relativní zeslabení kosti při 60 kV je 8, při 120 kV je 4. Takže vezmeme dvakrát radiogram při 120 kV a odečteme obraz při 60 kV. Takže pro kost dostáváme 2.4 – 8 = 0. Pro měkkou tkáň dostáváme 2.2 – 3 = 1. Grafické znázornění je uvedeno na obr. 3.

Obr. 3: Grafické znázornění odečtení kosti, včetně výsledného radiogramu (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

Podobně lze odečíst z radiogramů i měkkou tkáň, aby zůstaly znázorněné pouze kosti. Z obr. 2 víme, že relativní zeslabení měkké tkáně při 60 kV je 3, při 120 kV je 2. Takže vezmeme dvakrát radiogram při 60 kV a odečteme třikrát obraz při 120 kV. Takže pro měkkou tkáň dostáváme 2.3 – 3.2 = 0. Pro kost dostáváme 2.8 – 3.4 = 4. Grafické znázornění je uvedeno na obr. 4.

Obr. 4: Grafické znázornění odečtení kosti, včetně výsledného radiogramu (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

V současné době lze pro skiagrafii použitím dvou energií využít dvě CR kazety, mezi kterými bude vložen filtr. Při tomto řešení však není spektrální separace moc dobrá, viz obr. 5 vlevo. Pod pojmem spektrální separace rozumíme zobrazení dvěma rozdílnými spektry, aby byly součinitele zeslabení od sebe pokud možno co nejdále (aby mezi zelenou a červenou křivkou na obr. 1 byla co největší vzdálenost). Mimo horší spektrální separaci trpí tato technika také horší detekční kvantovou účinností ve srovnání s flat panel detektory. Existuje ještě jiné řešení, a to s použitím již zmíněného flat panel detektoru, takže DR techniky, kdy je první expozice provedena při napětí 120 kV a druhá expozice při energii 60 kV. Zde je již spektrální separace dostatečná, viz obr. 5 vpravo, avšak toto řešení může trpět pohybovými artefakty. A taktéž radiační zátěž pacientů bude pravděpodobně vyšší.

Obr. 5: Spektrální separace při dvou technikách s použitím duální energie (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

Ukázka radiogramů pořízených jak pomocí CR kazet a filtru, tak pomocí DR detektorů, jsou uvedeny na obr. 6 a 7.

Obr. 6: Radiogramy pořízené pomocí CR kazet s filtrem – standardní radiogram (vlevo), radiogram na měkké tkáně (uprostřed) a radiogram na kosti a kalcifikované léze (vpravo) (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

Obr. 7: Radiogramy pořízené pomocí DR detektoru s použitím dvou napětí – standardní radiogram (vlevo), radiogram na měkké tkáně (uprostřed) a radiogram na kosti a kalcifikované léze (vpravo) (https://www.upstate.edu/radiology/education/rsna/radiography/dual.php)

Všimněte si na obr. 6 úplně vlevo, že kalcifikované léze nejsou na standardním radiogramu tak zřejmé, jako na kostním radiogramu. Na obr. 7 na radiogramu pro měkké tkáně jsou viditelné měkkotkáňové léze, které na standardním radiogramu nejsou tak dobře viditelné.

Skiagrafie použitím dvou energií zatím není běžně používaná, ale již existují výrobci, kteří poskytují speciální detektory, které umožňují po každé expozici rekonstrukci tří radiogramů. Jeden standardní, jeden měkkotkáňový a jeden kostní. Jedná se např. o výrobce KA IMAGING INC (https://www.kaimaging.com/medical-solutions/reveal-35c-medical/) a speciálně pak detektor Reveal 35C. Ukázka několika standardních a následně zrekonstruovaných radiogramů je uvedena na obr. 8. Výrobce na svém webu samozřejmě poskytuje podstatně více radiogramů k nahlédnutí.

Obr. 8: Radiogramy pořízené s použitím detektoru Reveal 35 C výrobce KA IMAGING INC (https://www.kaimaging.com/medical-solutions/reveal-35c-medical/)

Z obrázků uvedených výše je zřejmé, že radiogramy pořízené při dvou energiích poskytují radiologům více informací, zvýrazňují některé léze, které by na standardním radiogramu byly hůře viditelné. Uvidíme časem, zda se tato technologie rozšíří, nebo zda zůstanou radiologové u klasických radiogramů pořízených s jednou energií, jako je tomu dosud…

Použitá literatura
https://www.upstate.edu/radiology/education/rsna/radiography/dual.php
https://www.kaimaging.com/medical-solutions/reveal-35c-medical/

CT generace – první, druhá a třetí

Napsat komentář

CT se vyvíjelo postupně, dosud existuje pět generací a ač se to zdá nepravděpodobné, vyšší pořadí generace neznamenalo nutně lepší CT skener, někdy bylo potřeba se ve vývoji vrátit o krok nazpět.

První generace CT se datuje do roku 1971 (takže je to letos přesně 50 let), kdy se pro náběr dat využívala kombinace translačního a rotačního pohybu, viz obr. 1 a 2. Využívalo se tužkového rtg svazku o rozměru 3 mm v axiálním směru (rovina XY) a 13 mm v podélném směru (odpovídá tloušťce řezu) s jedním protilehlým detektorem. Jako detektor se využíval scintilační detektor sodium jodid (NaI). Rekonstruované pole zájmu (FoV) bylo 24 cm, což umožňovalo provedení pouze CT skenu hlavy. Obrovskou nevýhodou byl velmi pomalý pohyb, jehož následkem byl čas potřebný pro jeden řez hlavou téměř 5 min. Výsledná matice měla velikost 80 px x 80 px, proto i prostorové rozlišení nebylo příliš dobré, přibližně 4 lp/cm. Tímto skenem bylo možné nahlédnout do anatomie pacienta a odlišit do té doby nevídané nízkokontrastní detaily. Obecně se však jednalo o významný pokrok v zobrazování. První CT obraz byl představen na kongresu Britské radiologické společnosti v roce 1972.

Obr. 1: První generace CT – translační pohyb (Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works)

Obr. 2: První generace CT – rotační pohyb (Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works)

V roce 1974 se objevila druhá generace CT, která stále kombinovala translační a rotační pohyb a využívala již mírně vějířového rtg svazku, viz obr. 3 a 4, náběr dat byl rychlejší. V počátcích zahrnovaly CT skenery pouze tři detektory, takže získání dat pro jeden řez hlavou trval přibližně 2 min (cca 3x rychlejší než pro 1. generaci CT). Pokročilejší CT skenery druhé generace již měly i více než 30 detektorů, čemuž odpovídal úhel vějířového svazku okolo 10°. To umožnilo velké urychlení náběru dat, pro náběr dat jednoho řezu postačovala doba kratší než 20 s.

Obr. 3: Druhá generace CT – translační pohyb (Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works)

Obr. 4: Druhá generace CT – rotační pohyb (Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works)

Krátce na to, již v roce 1975, se objevila třetí generace CT, která využívala pouze rotačního pohybu rentgenky a detektorů a vějířového rtg svazku s úhlem v rozmezí 45-55°, viz obr. 5 a 6. Doba náběru dat se výrazně zkrátila, čas potřebný pro získání dat jednoho řezu byl okolo jedné sekundy. U této generace byla rentgenka pevně spojena s protilehlými detektory, kterých bylo přibližně 300 u CT skenerů v počátcích třetí generace a okolo 700 v pozdějších fázích třetí generace. Detektory byly umístěny na části kružnice a rotovaly společně s rentgenkou. Nevýhodou této generace byl však vznik kruhových artefaktů. Ale proč netrpěly kruhovým artefaktem také předchozí generace? Na chvíli se zde zastavme a vraťme k první a druhé generaci. U těchto dvou generací byl vlastně každý detektor kalibrován na začátku každého translačního pohybu (jednalo se o dynamickou kalibraci), protože bylo možné zjistit jeho odezvu na ozáření, při kterém rtg svazek neprochází pacientem. Ale u třetí generace to již možné nebylo, některé detektory (typicky ty uprostřed) nejsou nikdy ozářeny nezeslabeným rtg svazkem, takže nebylo možné provést dynamickou kalibraci při každém skenu. Proto třetí generace CT vyžadovala extrémně dobrou stabilitu CT detektorů. Špatně kalibrovaný detektor, klidně jen s nepřesností 0,1 %, pak měl za následek vznik onoho zmíněného kruhového artefakt.

Obr. 5: Třetí generace CT – rotační pohyb (Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works)

Obr. 6: Třetí generace – rotační pohyb – ukázka z jiného směru (Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works)

V příštím příspěvku budeme pokračovat dalšími generacemi CT skenerů.

Použitá literatura
Flohr T. CT Systems. Curr Radiol Rep 1, 52–63 (2013). https://doi.org/10.1007/s40134-012-0005-5
Goldman LW. Principles of CT and CT technology. J Nucl Med Technol. 2007;35(3):115-130. doi:10.2967/jnmt.107.042978
Animated CT Generations [1st, 2nd, 3rd, 4th, 5th Gen CT] For Radiologic Technologists • How Radiology Works

Kvíz XVI – pokročilejší

Napsat komentář

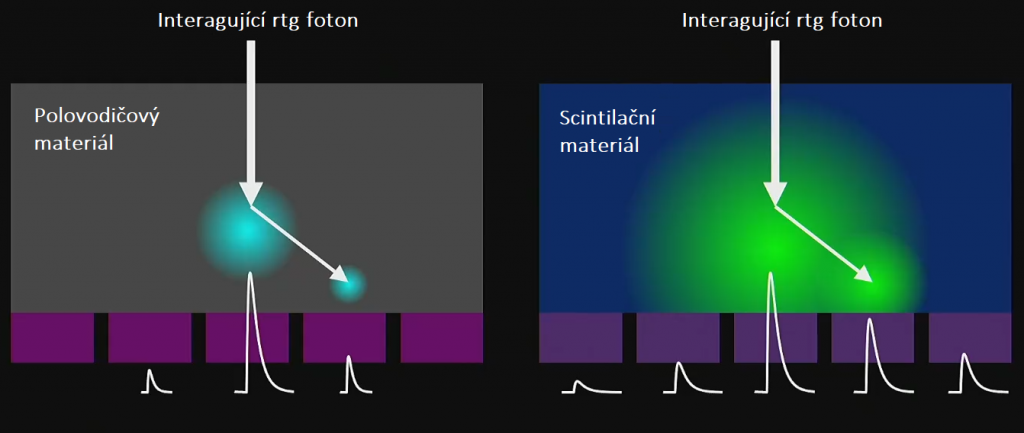
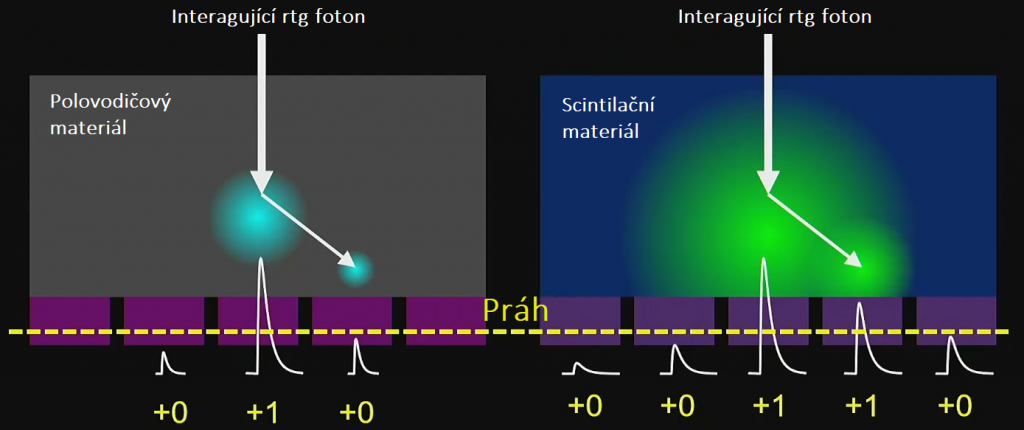
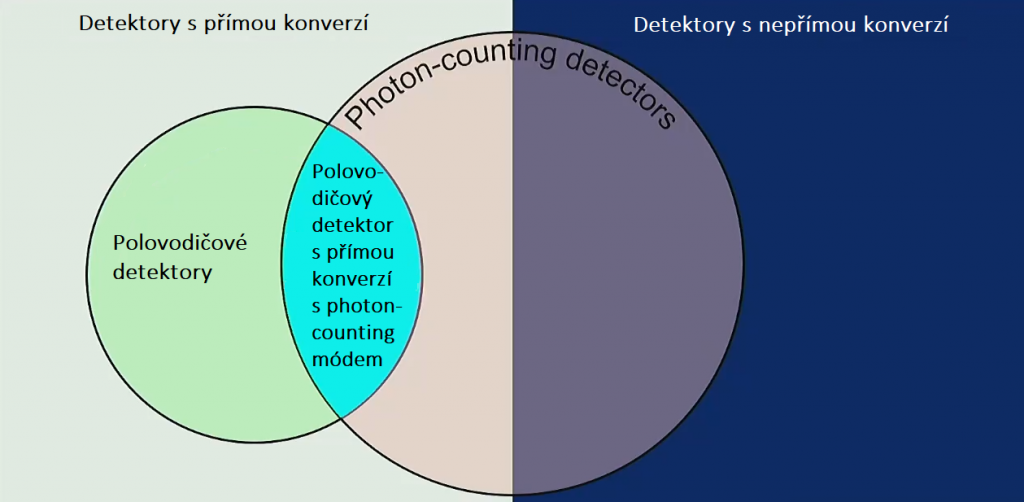
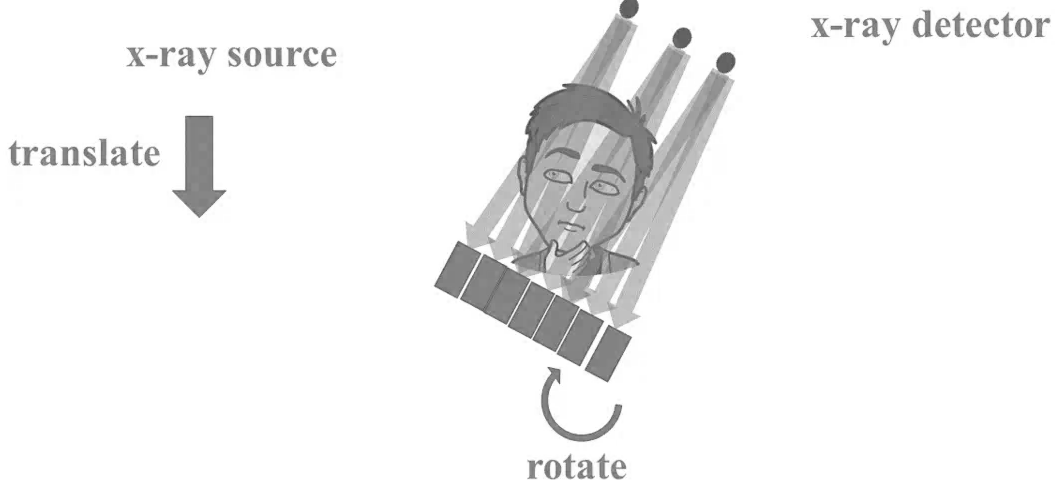
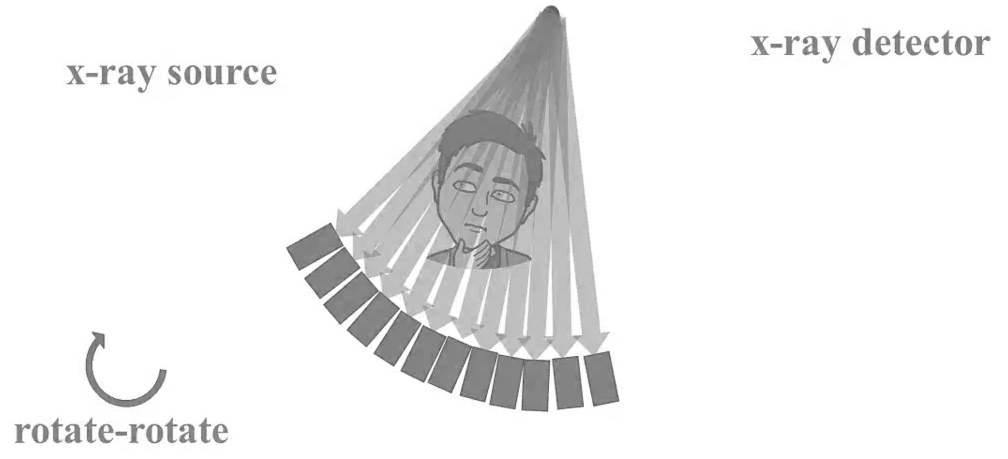
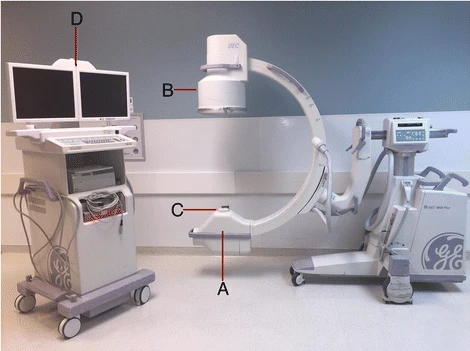
Kvíz se týká tomografického zobrazení – MDCT = multi-detector CT (klasické CT), CBCT = cone-beam CT (angiografické systémy, zubní CBCT).

Otázky:
Q1: Z jak velkého úhlu jsou standardně nabírána data u MDCT (mimo kardiologická vyšetření)?
a) 90°
b) 180°
c) 180° + fan beam
d) 360°

Q2: Z jak velkého úhlu jsou standardně nabírána data u MDCT pro kardiologická vyšetření?
a) 90°
b) 180°
c) 180° + fan beam
d) 360°

Q3: Co mění automatická modulace proudu u MDCT na základě zeslabení pacienta?
a) Dobu rotace
b) Napětí
c) Anodový proud
d) Elektrické množství

Q4: Co mění automatická volba napětí u MDCT na základě zeslabení pacienta?
a) Dobu rotace
b) Napětí
c) Anodový proud
d) Elektrické množství

Q5: Jak společně funguje automatická modulace proudu a automatická volba napětí u MDCT v závislosti na zeslabení pacienta?
a) Po celou dobu skenu se mění proud a napětí
b) Po celou dobu skenu se drží jedna hodnota proudu a mění se napětí
c) Po celou dobu skenu se mění proud a drží se jedna hodnota napětí
d) Po celou dobu skenu se drží jedna hodnota proudu a napětí

Q6: Na základě kterého parametru lze odlišit MDCT od CBCT?
a) U MDCT obíhá rentgenka okolo pacienta o 360°, zatímco u CBCT nikoliv
b) U CBCT je maximální kolimace vždy menší než u MDCT
c) U CBCT je maximální kolimace vždy větší než u MDCT
d) U MDCT je dávka pacientovi vždy nižší než u CBCT

Q7: Jaká je typická doba rotace (s) u MDCT a jaká u CBCT?
a) 0,2-1 s u MDCT, 1-5 s u CBCT
b) 0,2-1 s u MDCT, 5-10 s u CBCT
c) 1-5 s u MDCT, 1-5 s u CBCT
d) 1-5 s u MDCT, 5-10 s u CBCT

Q8: Jak většinou souvisí počet řezů uváděný výrobcem s reálným počtem detektorových řad?
a) Počet řezů ≥ počet detektorových řad
b) Počet řezů = počet detektorových řad
c) Počet řezů ≤ počet detektorových řad
d) Nelze jednoznačně říct

Q9: S menším rekonstruovaným field of view (FoV) dochází v CT obraze ve srovnání s větším rekonstruovaným FoV:
a) Ke snížení šumu
b) Ke zvýšení šumu
c) Žádná změna
d) Nelze obecně říci

Q10: Jaká je přibližně velikost detekčního elementu u MDCT?
a) 0,05-0,1 mm
b) 0,1-0,2 mm
c) 0,2-0,6 mm
d) 0,6-1,0 mm

Q11:  Jaká je přibližně velikost detekčního elementu u angiografického CBCT?
a) 0,05-0,1 mm
b) 0,1-0,2 mm
c) 0,2-0,6 mm
d) 0,6-1,0 mm

Q12: Jak je definována velikost detekčního elementu u MDCT?
a) Je to reálná velikost detekčního elementu
b) Je to velikost detekčního elementu ve vzdálenosti 15 cm od izocentra směrem k rentgence
c) Je to velikost detekčního elementu ve vzdálenosti 15 cm od izocentra směrem od rentgenky
d) Je to velikost detekčního elementu v izocentru

Q13:  Jak je definována velikost detekčního elementu u CBCT?
a) Je to reálná velikost detekčního elementu
b) Je to velikost detekčního elementu ve vzdálenosti 15 cm od izocentra směrem k rentgence
c) Je to velikost detekčního elementu ve vzdálenosti 15 cm od izocentra směrem od rentgenky
d) Je to velikost detekčního elementu v izocentru

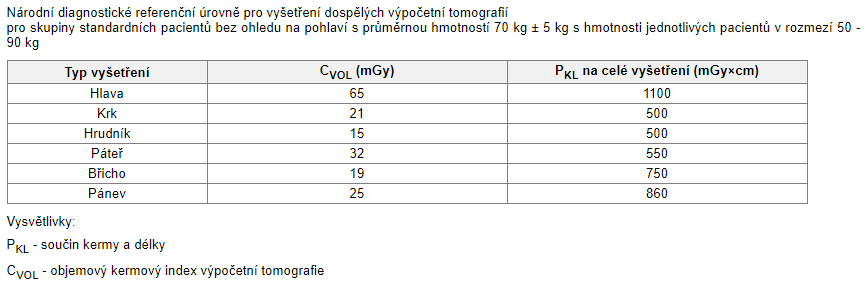
Q14: Množství vyprodukovaného záření na jednu rotaci je u MDCT kvantifikováno pomocí parametru CTDI_vol, který může být stanoven pro malý PMMA fantom o průměru 16 cm nebo pro velký PMMA fantom o průměru 32 cm. Jaký je přibližný vztah mezi CTDI_vol v malém a velkém fantomu při stejných expozičních parametrech?
a) CTDI_vol (malý) ≈ 1/2*CTDI_vol (velký)
b) CTDI_vol (malý) ≈ CTDI_vol (velký)
c) CTDI_vol (malý) ≈ 2*CTDI_vol (velký)
d) CTDI_vol (malý) ≈ 3*CTDI_vol (velký)

Q15: Jak se mění u MDCT s danou referenční kvalitou obrazu a tedy zapnutou automatickou modulací proudu dávka pacientovi (resp. CTDI_vol) v závislosti na rostoucím pitch faktoru?
a) S rostoucím pitch faktorem dávka pacientovi klesá
b) S rostoucím pitch faktorem dávka pacientovi zůstává přibližně stejná
c) S rostoucím pitch faktorem dávka pacientovi narůstá
d) Nelze jednoznačně říci

Q16: Jaký anodový proud bychom museli použít u MDCT skenu s parametry – rotační čas 0,5 s; pitch faktor 1,2; CTDI_vol 0,95 mGy, abychom dostali stejnou kvalitu obrazu jako při skenu s pitch faktorem 0,35; anodovým proudem 35 mA; rotačním časem 0,5 s a CTDI_vol 0,95 mGy?
a) 10 mA
b) 50 mA
c) 120 mA
d) 150 mA

Q17: Existují dva základní přístupy k nastavení automatické modulace proudu. První přístup je, že se CT skener snaží udržet poměr kontrast/šum konstantní. Druhý přístup je, že se zvyšuje akceptovatelný šum s rostoucí velikostí pacienta. Který z přístupů je šetrnější z pohledu dávky pacientovi?
a) První přístup
b) Druhý přístup
c) Nelze jednoznačně říci

Q18: Jaké je vysvětlení druhého přístupu v předešlé otázce? Proč je u větších pacientů akceptovatelnější vyšší šum?
a) Protože si radiolog zvykne
b) Protože to musí tak být kvůli akceptovatelné dávce pacientovi
c) Protože obéznější pacienti obsahují více subkutánního tuku, který lépe odděluje orgány od sebe
d) Protože obéznější pacienti obsahují více viscerálního tuku, který lépe odděluje orgány od sebe

Q19: S měnící se hodnotou napětí u MDCT se mění kvalita obrazu. Jakým způsobem? Doplňte následující tvrzení: S vyšší hodnotou napětí…:
a) Roste kontrast a klesá šum
b) Roste kontrast, ale i šum
c) Klesá kontrast a roste šum
d) Klesá kontrast, ale i šum

Q20: Které z následujících typů MDCT vyšetření bude nejvíce profitovat z nižší hodnoty napětí použitého při CT skenu?
a) Angiografické vyšetření
b) Nativní vyšetření
c) Postkontrastní vyšetření
d) Všechna vyšetření stejně

Q21: Lokalizační sken je možné pořídit v různých projekcích, typicky se využívá AP, ale je možné také PA nebo LAT. Jak ovlivňuje projekce lokalizačního skenu fungování automatické modulace proudu z hlediska hodnoty CTDI_vol u většiny výrobců?
a) Při AP lokalizačním skenu je CTDI_vol nejvyšší
b) Při PA lokalizačním skenu je CTDI_vol nejvyšší
c) Při LAT lokalizačním skenu je CTDI_vol nejvyšší
d) Při kombinaci AP a LAT lokalizačním skenu je CTDI_vol nejvyšší

Q22: Co se děje s kvalitou CT obrazu, je-li průměr vyšetřovaného pacienta větší než maximální velikost rekonstruovaného FoV?
a) Nic, nemá to vliv, hlavně že se pacient vejde do gantry
b) Zhoršuje se – vyšší šum
c) Zhoršuje se – vznik artefaktů
d) Zlepšuje se, protože využíváme větší oblast v gantry

Q23: Jakým způsobem lze redukovat kovové artefakty?
a) Zvýšit napětí a použít algoritmus pro redukci kovových artefaktů
b) Zvýšit napětí a zvýšit proud
c) Zvýšit proud a použít algoritmus pro redukci kovových artefaktů
d) Použít algoritmus pro redukci kovových artefaktů

Q24: Podstupuje-li CT vyšetření obézní pacientka, která má navíc objemná prsa, může se stát, že má prsa po stranách hrudníku, mimo rekonstruované FoV. Jakým způsobem by v takovém případě měl být proveden sken?
a) Nijak, takovou pacientku nevyšetřovat
b) Zvýšit napětí
c) Centrovat pacientku pod izocentrum
d) Doporučit pacientce, aby si vzala podprsenku, aby měla pokud možno co nejvíce kruhový průřez

Q25: Orgánová modulace proudu modifikuje použitý anodový proud v závislosti na projekci. V jakých projekcích (pozicích) rentgenka neprodukuje záření? Projekce (pozice) jsou popsány pomocí ručiček na hodinovém ciferníku.
a) 2-6
b) 6-10
c) 10-2
d) 12-4

Q26: Kterému orgánu lze použitím automatické modulace proudu ušetřit dávku?
a) Plicím
b) Kůži
c) Prsní tkáni
d) Mozku

Q27: U kterých CT výkonů je zpravidla dosahováno vyšší radiační zátěže pacientů, než je obvyklé?
a) CT mozku nativní a kontrastní
b) CT angiografie mozkových tepen
c) Dual energy CT mozku
d) CT perfuze mozku

Q28: Jak se mění CT číslo vody s rostoucí hodnotou napětí?
a) Klesá
b) Roste
c) Zůstává stejné
d) Nelze jednoznačně říct

Q29:Jak se mění CT číslo kontrastní látky s rostoucí hodnotou napětí?
a) Klesá
b) Roste
c) Zůstává stejné
d) Nelze jednoznačně říct

Q30: Jak se změní kvalita obrazu, jestliže změníme velikost rekonstruovaného FoV z 20 cm x 20 cm na 35 cm x 35 cm?
a) Zlepší se prostorové rozlišení a sníží se šum
b) Zlepší se prostorové rozlišení, ale zvýší se šum
c) Zhorší se prostorové rozlišení, ale sníží se šum
d) Zhorší se prostorové rozlišení a zvýší se šum

Odpovědi:
A1: d) 360°
A2: c) 180° + fan beam
A3: c) Anodový proud
A4: b) Napětí
A5: c) Po celou dobu skenu se mění proud a drží se jedna hodnota napětí (ačkoliv si spousta lidí myslí, že se mění po celou dobu skenu proud i napětí, tak tomu tak není, mění se pouze proud a hodnota napětí se zvolí na začátku podle lokalizačního skenu a zůstává po celou dobu skenu stejná)
A6: a) U MDCT obíhá rentgenka okolo pacienta o 360°, zatímco u CBCT nikoliv
A7: b) 0,2-1 s u MDCT, 5-10 s u CBCT
A8: a) Počet řezů ≥ počet detektorových řad
A9: b) Ke zvýšení šumu (v každém voxelu je při menším rekonstruovaném FoV méně rtg fotonů, proto vyšší šum)
A10: c) 0,2-0,6 mm
A11: b) 0,1-0,2 mm
A12: d) Je to velikost detekčního elementu v izocentru (takže reálná velikost detekčního elementu o velikosti 0,6 mm v izocentru je při zvětšení 1,5x 0,9 mm)
A13: a) Je to reálná velikost detekčního elementu
A14: c) CTDI_vol (malý) ≈ 2*CTDI_vol (velký)
A15: b) S rostoucím pitch faktorem dávka pacientovi zůstává přibližně stejná
A16: c) 120 mA (jde nám o dosažení stejné hodnoty efektivní mAs = mA*rotační čas/pitch, tedy 35*0,5/0,35 = 50 mAs, pro rotační čas 0,5 s a pitch faktor 1,2 pak musíme použít proud 120 mA)
A17: b) Druhý přístup
A18: d) Protože obéznější pacienti obsahují více viscerálního tuku, který lépe odděluje orgány od sebe
A19: d) Klesá kontrast, ale i šum
A20: a) Angiografické vyšetření
A21: b) Při PA lokalizačním skenu je CTDI_vol nejvyšší (ano, je to tak, existuje celá řada studií, např. Effect of CT Localizer Radiographs on Radiation Dose Associated With Automatic Tube Current Modulation: A Multivendor Study – ScienceDirect, které to dokazují, proto je výhodnější provádět lokalizační sken v AP projekci; v případě dvou lokalizačních skenů by druhý sken měl být v AP projekci)
A22: c) Zhoršuje se – vznik artefaktů
A23: a) Zvýšit napětí a použít algoritmus pro redukci kovových artefaktů
A24: d) Doporučit pacientce, aby si vzala podprsenku, aby měla pokud možno co nejvíce kruhový průřez
A25: c) 10-2 (rentgenka neprodukuje záření v horních 120°)
A26: c) Prsní tkáni
A27: d) CT perfuze mozku
A28: c) Zůstává stejné
A29: a) Klesá
A30: b) Zlepší se prostorové rozlišení, ale zvýší se šum

Mobilní CT

Napsat komentář

Pod pojmem „mobilní CT“ se mohou skrývat dva významy, které se však v českém překladu ztrácí. Významy sousloví mobilní CT mohou být následující:

  1. Jedná o CT na kolečkách (viz obr. 1), které může přejíždět v rámci nemocnice mezi různými odděleními.
  2. Jedná se o klasické CT, které je umístěno v návěsu (viz obr. 2), který s připojením k tahači projíždí méně dostupné geografické oblasti a provádí se na něm CT vyšetření obyvatel, kteří to ke klasickému CT skeneru mají velmi daleko, většinou desítky hodin cesty. Nebo se jedná o pacienty s komplikovaným socioekonomickým zázemím, kteří by na vzdálenější CT nejeli. Typickou zemí, kde několik pojízdných CT existuje, jsou Spojené státy americké. Nejčastěji se však jedná o mobilní CT skenery pro screening plic kuřáků a v dnešní době případně také mobilní CT skenery pro skenování covid pozitivních pacientů. V Evropě mobilní CT rozšířena nejsou.

Obr. 1: Mobilní CT [NeuroLogica | Medical Imaging Technology]

Obr. 2: Klasické CT umístěné v pojízdném návěsu [Mobile CT | Infectious Disease CT Solution | Computed Tomography – CT Scanners | Canon Medical Systems USA]

S každým z výše popsaných mobilních CT je spojeno několik výhod i nevýhod. V praxi jde vždy o to, o jaké konkrétní použití se jedná, aby byla uváženy právě ony výhody a nevýhody.

Ad 1. Mezi výrobce mobilních CT patří Neurologica, která se již v roce 2015 objevila na trhu s mobilním CT skenerem, který byl určen pro radiologická vyšetření hlavy a krku především z neurochirurgických indikací, proto i průměr otvoru v gantry byl tomu uzpůsoben (32 cm). Výhodou těchto skenerů byla právě jejich mobilita, kdy nebylo potřeba v rámci neurochirurgických operačních výkonů přejíždět s pacientem z operačního sálu na CT vyšetřovnu. Výhodou také byla možnost provést CT vyšetření přímo u pacientova lůžka, aniž se musel složitě překládat a převážet v rámci nemocnice. Avšak přeprava CT skeneru v rámci nemocnice může být poněkud komplikovanější, CT váží přes 400 kg a kvůli rozměrům může být někdy obtížnější projet některými užšími chodbami. Novější CT pak váží dokonce i přes 700 kg. Další nevýhodou těchto CT skenerů je jejich výkon, obecně se dá říct, že žádný z nabízených mobilních CT skenerů není ani zdaleka srovnatelný s klasickými CT skenery. Avšak i tak samozřejmě je možné na mobilních CT skenerech získat CT obrazy s diagnostickými informacemi.

Přehled mobilních CT skenerů pro vyšetření mozku (hlavy):
CereTom Elite (Neurologica) – otvor  gantry 32 cm, 8-řadý solid-state detektor, detekční element 1,25 mm, doba rotace 2 s, napětí 100-140 kV, anodový proud 1-7 mA, hmotnost 438 kg (další informace).
OmniTom (Neurologica) – otvor gantry 40 cm, 16-řadý GOS detektor, detekční element 0,625 mm, doba rotace 1 s, napětí 70-120 kV, anodový proud 5-45 mA, hmotnost 726 kg (další informace).
SOMATOM On.site (Siemens) – otvor gantry 35 cm, 32-řadý Stellar detektor, detekční element 0,75 mm, doba rotace 1 s, napětí 80-120 kV, anodový proud 3-24mA, hmotnost 998 kg (další informace).

Mimo mobilní CT pro vyšetření hlavy a krku jsou na trhu dostupné také CT skenery s velkým průměrem gantry, aby bylo možné vyšetřit celé tělo pacienta. Na těchto CT je možné vyšetřit hlavně statické části lidského těla, typicky vše mimo srdce. Na CT skenery jsou pro zobrazení srdce kladeny velmi vysoké požadavky, které samozřejmě takové mobilní CT nesplňuje.

Přehled mobilních CT skenerů pro vyšetření celého těla:
BodyTom Elite (Neurologica) – otvor gantry 85 cm (FoV neuvěřitelných 60 cm), 32-řadý solid-state detektor, detekční element 1,25 mm, doba rotace 1 s, napětí 80-140 kV, anodový proud 50-300 mA, hmotnost 1592 kg (další informace).

Je možné, že existuje více mobilních CT skenerů pro vyšetření celého těla, ale nemám o nich informace.

Ad 2. Výhodou klasických CT umístěných v návěsu s tahačem je to, že se jedná o klasické CT, tedy s velkým výkonem, krátkou dobou rotace (sub-sekundové časy), s velkou celkovou kolimací. Nevýhodou je nutnost častých kontrol kvality, protože CT přece jen dost trpí neustálým pojížděním v terénu. Vezmeme-li si, že kvalitní CT je založeno na přesné fokuzaci svazku elektronů z katody na anodu, pak jízda v hrbolatém terénu může způsobit dost škody. To je hlavní nevýhoda těchto mobilních CT.

Při psaní tohoto příspěvku jsem narazila na americkou společnost, která pronajímá CT skenery v návěsu. Jedná se o kvalitní CT skenery výrobců GE (Revolution Discovery 750HD, 750HD a VCT 64/128), Toshiba/Canon (Aquilion Prime SP 80, Aquilion Prime 160, Aquilion VeloCT a Aquilion 64 Whole Body) a Siemens (Somatom Perspective 64/128). Podle informací na webu možnosti pronájmu CT skeneru již využilo několik pracovišť, hlavně z důvodu vyšší poptávky po CT vyšetření u covidových pacientů.

U CT skenerů v návěsu ještě existuje několik možností přemístění, ne všechny CT v návěsu jsou připojeny k tahači. Buď se tedy jedná o CT v návěsu s možným připojením k tahači (obr. 3 vlevo), nebo se jedná o hybridní typ (obr. 3 uprostřed), u kterého se předpokládá, že takový skener zůstanu na místě po delší dobu, např. 3-6 měsíců, nebo se jedná o trvalý typ (obr. 3 vpravo), který lze instalovat s použitím jeřábu a v takovém případě se jedná o rozšíření prostor nemocnice o novou buňku, ve které je takový skener instalovaný.

Obr. 3: CT v návěsu s možným připojením k tahači (vlevo), hybridní typ umístění na dobu min. 3-6 měsíců (uprostřed) a trvalý typ (vpravo) [Lamboo medical (lamboo-medical.com)]

Poznámka: Neurologica byla pravděpodobně koupena firmou Samsung, takže některé výše zmíněné CT skenery jsou na webu dohledatelné i pod výrobcem Samsung. Ale myslím si, že to není pro pochopení příspěvku podstatné.

Webinář IAEA – zdůvodnění a optimalizace dentálního 2D a 3D zobrazení

Napsat komentář

International Atomic Energy Agency organizuje dne 21. 5. 2021 webinář na téma Zdůvodnění a optimalizace dentálního 2D a 3D zobrazení. Pro více informací: Improved justification and optimization of dental 2D and 3D imaging through education and training | IAEA. Webinář je přístupný zdarma po registraci.

Aktuální webináře

Napsat komentář

Do záložky Vzdělávání / Webináře bylo přidáno několik odkazů na aktuálně pořádané webináře, které se týkají radiodiagnostiky a intervenční radiologie.

Přehled aktuálních

International Organisation for Medical Physics (IOMP)
IOMP School Webinars – International Organization for Medical Physics. Semináře je možné sledovat také retrospektivně, za rok 2021 a za rok 2020.

European Federation of Organisations for medical Physics (EFOMP)
EFOMP :: Webinar Series 2020-2021

Fluoroscopy Users‘ Group (FLUG)
Masterclass Webinar Series – Fluoroscopy Users‘ Group (flug.org.uk)

International Atomic Energy Agency (IAEA)
Webinars in radiation protection | IAEA – radiační ochrana obecně, je potřeba si vybrat vhodný seminář. Semináře je možné sledovat také retrospektivně.

Radiační ochrana při operačních výkonech v ortopedii

Napsat komentář

International Atomic Energy Agency [1] nedávno na svém webu uveřejnila informace o radiační ochraně v ortopedii, společně s přehledem efektivních dávek u nejčastěji prováděných výkonů. Proto dnešní delší příspěvek bude zaměřen na toto téma také.

Skiaskopie se již stala nezbytnou součástí ortopedických operačních výkonů. Nejčastěji používaným rtg systémem je pojízdné C-rameno, které se pohybuje v rámci i několika operačních sálů a je používáno různými lékaři. Bohužel stále platí, že znalosti ohledně správného a bezpečného používání rtg záření nejsou mezi lékaři dostatečné [2].

Osobní dávky lékařů ani dávky pacientů z ortopedických výkonů s použitím C-ramene zdaleka nedosahují tak vysokých hodnot jako v případě intervenčních radiologických a kardiologických výkonů. Primárně díky tomu, že se nejedná o plně skiaskopicky naváděné výkony (ortoped využívá skiaskopii pouze ve velmi omezené míře) s prováděním akvizičních scén, případně digitální subtrakční angiografie. I přesto je však na místě dodržovat zásady radiační ochrany.

Mezi základní pravidla patří jednoznačně použití osobních ochranných pomůcek, zejména ochranných zástěr a ochranných límců. Ke zlepšení klinické praxe napomáhá vhodné teoretické vzdělání – jak rtg systém funguje, jakým způsobem vzniká rtg obraz, čím lze ovlivnit kvalitu obrazu a v neposlední řadě také jak lze ovlivnit dávku pacientovi i samotnému lékaři. Pozitivní vliv má také dobrá komunikace s radiologickým asistentem, jehož přítomnost při používání C-ramene je v mnoha zemích vyžadována.

Ačkoliv se použití ochranných pomůcek a teoretické vzdělání mohou zdát samozřejmé, tak irská studie [2] ukázala, že 65 % ortopedů v přípravě nemá v průběhu vzdělávání ani základní kurz radiační ochrany, 96 % ortopedů sice používá ochrannou zástěru, ale podstatně menší část používá také ochranný límec.

Jiná studie, tentokrát provedená v Anglii a Walesu [3], ukázala, že přestože existuje spousta studií o použití záření v ortopedii, pouze 8 z 50 lékařů ve výcviku některou studii četlo. Studie [3] také ukázala, že většina lékařů si není vědoma, že oblastí s nejvyššími dávkami na těle ortopeda jsou ruce (vědělo pouze 50 %). 32 % lékařů považuje za oblast s nejvyššími dávkami hlavu, 12 % trup a 6 % oči.

Ve studii [4] autor doporučuje provést u traumatických pacientek ve fertilním věku těhotenský test. Asi je to poněkud zvláštní přístup na dnešní dobu, pokud je to akutní stav, pak asi nebude čas provést test. I kdyby byl pozitivní, tak pokud je to akutní stav, tak se výkon s použitím rtg stejně provede. Zpětně se pak provede odhad dávky na plod a podle fáze těhotenství a dávky na plod se rozhodne o dalším postupu. Dávky na plod u těchto výkonů, kdy je použita často pouze skiaskopie (ale klidně po dobu několika minut), jsou relativně nízké. Prahová hodnota dávky na plod pro výskyt tkáňových (deterministických) účinků je docela vysoká, takže u většiny skiaskopických výkonů se prahové dávky nedosáhne.

Základní informace o C-ramenu a ochraně před zářením
Mezi základní součásti zobrazovacího řetězce u C-ramene patří rentgenka (zdroj záření), receptor obrazu (flat panel detektor nebo zesilovač obrazu – u starších nebo levnějších C-ramen), kolimátor a displej pro zobrazení rtg obrazu. Základní součásti jsou ilustračně znázorněny na obr. 1. Rentgenka produkuje záření, kolimátor upravuje velikost primárního rtg svazku, receptor obrazu detekuje záření prošlé pacientem a tvoří obraz, který se pak zobrazí na displeji.

Obr. 1: Základní součásti zobrazovacího řetězce (A – rentgenka, B – receptor obrazu, C – kolimátor, D – displej) [2]

Jen pro informaci ukázka, jak vypadá s C-rameno s flat panel detektorem a jak se zesilovačem obrazu, je uvedena na obr. 2.

Obr. 2: C-rameno s flat panel detektorem (vlevo) a se zesilovačem obrazu (vpravo)

Rentgenka generuje záření, které dopadá na pacienta, interaguje v pacientovi, velká část se pohltí, menší část se rozptýlí v pacientovi a také vyletí ven z pacienta (a ozáří pracovníky) a ještě menší část prochází pacientem a dopadá na receptor obrazu. Z těch poté vzniká rtg obraz.

Jakmile záření dopadne na pacienta, velká část záření se z pacienta rozptýlí zpětně, jak je uvedeno na obr. 3. Kvůli tomuto zpětnému rozptylu se doporučuje, aby, pokud je to možné, byla rentgenka umístěna pod pacientem, tedy pod stolem s pacientem. V takovém případě pak rozptýlené záření putuje k zemi a způsobuje staticky významně menší ozáření lékařů než v případě, kdy je rentgenka umístěna nad pacientem. Znázornění rozptýleného záření pro obě pozice rentgenky je znázorněno na obr. 3 červenými šipkami.

Obr. 3: Znázornění rozptýleného záření při pozici rentgenky pod pacientem (vlevo) a nad pacientem (vpravo) [2]

Množství rozptýleného záření a radiační zátěž z toho plynoucí pro lékaře lze redukovat zmenšením velikost rtg pole (správná kolimace, viz obr. 4), zmenšením prozařovaného objemu (co nejméně používat šikmé a bočné projekce, používat zadopřední) a také snížením napětí (na C-ramenech s expoziční automatikou manuální nastavení napětí většinou není možné, systém si ho volí automaticky). Současně s tím lze uplatnit všechna tři základní pravidla radiačních ochrany – ochrana vzdáleností (poodstoupení od pacienta, je-li to možné), ochrana stíněním (osobní ochranné prostředky, samostatně stojící stínící bariéry) a ochrana časem (čím kratší dobu se používá rtg záření, tím menší dobu jsem v rozptýleném záření, tím lépe).

Obr. 4: Nedostatečná kolimace (vlevo) a správná kolimace (vpravo) [2]

Autoři některých publikací doporučují při vkládání rukou do primárního rtg svazku použití ochranných rukavic se stínicím ekvivalentem. To však není vždy správná volba, protože jakmile ruka s rukavicí překryje aktivní oblast expoziční automatiky (oblast, ze které rtg systém na základě množství prošlého záření vyhodnocuje, je-li potřeba dávku zvýšit nebo snížit), rtg systém to vyhodnotí jako více zeslabující objekt a dávku zvýší. Toto zvýšení bude vyšší než v případě, že aktivní oblast expoziční automatiky překryje pouze ruka samotná (myšleno bez rukavice). Při použití rukavice sice dojde ke snížení dávky na ruku, ale tím, že dojde ke zvýšení dávky kvůli více zeslabujícímu objektu, je pak ušetřená dávka na ruce opravdu velmi nízká.

Dalším základním přístupem vedoucím k redukci dávek je použití pulzní skiaskopie (což je pro většinu pracovišť naprostá samozřejmost), redukce délky a počtu skiaskopických smyček (scén) a současně redukce počtu pulzů za sekundu. Standardně by to mělo být v rozsahu 1-6 pulzů/s, zatímco kontinuální skiaskopie používá 30 p/s. U akvizice, je-li použita (kvalitnější zobrazení s podstatně vyšší dávkou) se doporučuje používat single akvizice (pořízení pouze jednoho obrazu místo celé smyčky), je-li to možné a také minimalizovat počet obrazů při delší akvizici.

Většinu výše zmíněných způsobů k redukci radiační zátěže lze aplikovat současně, jedná se o přístup k ozáření jako takovému. Kdykoliv, kdy se využívá rtg záření, měl by ortoped pamatovat na základní princip ALARA – As Low As Reasonably Achievable – tak nízko, jak je rozumně dosažitelné. Tedy nedělat ze záření zabijáka a nestát v betonovém bunkru, ale ani nepoužívat záření víc, než je nezbytně nutné.

Použitá literatura
[1] Radiation protection of medical staff in orthopedic surgery | IAEA
[2] Kaplan DJ, Patel JN, Liporace FA, et al. Intraoperative radiation safety in orthopaedics: a review of the ALRA (As low as reasonably achievable) principle. Patien Saf Surg. 2016; 10: 27.
[3] Khan FR, Ul-Abadin Z, Rauf S, et al. Awareness and attitudes amongst basic surgical trainees regarding radiation in orthopaedic trauma surgery. Biomed Imaging Interv J 2010; 6(3): e25.
[4] Flik K, Kloen P, Toro JB, et al. Orthopaedic trauma in the pregnant patients. J Am Acad Orthop Surg. 2006; 14(3): 175-82.

Nové tutoriály na webu International Atomic Energy Agency

Napsat komentář

IAEA přidala na svůj web několik tutoriálů.

Jeden se týká QC na CT, je k dispozici zde: Human Health Campus – Tutorial Videos on Quality Control for CT (iaea.org). Tutoriál se skládá z několika krátkých videí, ve kterých je popsáno a  ilustrativně předvedeno, co se daným testem ověřuje, jak se test provádí, jak se vyhodnocuje a taktéž jaké odchylky jsou ještě akceptovatelné (dle doporučení Quality Assurance Programme for Computed Tomography: Diagnostic and Therapy Applications | IAEA). Tato publikace je také velmi užitečná jako návod pro provádění QC na CT skenerech.

Dále je na webu IAEA k dispozici tutoriál pro Radiační ochranu u intervenčních výkonů, k dispozici zde: Online training in radiation protection | IAEA , kdy je potřeba se registrovat, ale současně je možné získat certifikát. Individuální videa jsou pak přístupná zde: Training material | IAEA, videa komprimovaná v jednom zip souboru pak zde: rpop_radiation_protection_in_interventional_procedures.zip | IAEA.

Mimo výše zmíněné byl na web IAEA umístěn také vzdělávací tutoriál pro Radiační ochranu při zobrazování v dentální radiologii, který je k dispozici zde: Online training in radiation protection | IAEA. Opět možné shlédnout buď s registrací a certifikátem, nebo volně bez registrace.

Kvíz XV

2 komentáře

Kvíz se týká CT zobrazení a CT vyšetření.

Otázky:
Q1: Která z následujících vlastností není vlastností bow tie filtru?
a) Redukuje intenzitu svazku, která dopadá na detektor
b) Dělá šum uniformnější
c) Kolimuje rtg svazek dopadající na pacienta
d) Zvyšuje průměrnou energii dopadajícího svazku

Q2: U typického jednořadého CT skeneru je tloušťka řezu určena:
a) Velikostí ohniska
b) Šířkou rtg svazku
c) Velikosti zeslabující protirozptylové mřížky
d) Šířkou bow tie filtru

Q3: U typického multidetektorového CT skeneru je tloušťka řezu určena:
a) Velikostí ohniska
b) Šířkou rtg svazku
c) Šířkou individuálního detektoru a tím, jsou-li informace sousedních detekčních elementů kombinovány
d) Šířkou bow tie filtru

Q4: u CT skiaskopie se
a) Stůl kontinuálně pohybuje, ale rentgenka je stacionární
b) Stůl je stacionární, ale rentgenka se kontinuálně pohybuje
c) Stůl i rentgenka se kontinuálně pohybují
d) Stůl i rentgenka jsou stacionární

Q5: Které z následujících tvrzení o cone-beam svazku je nepravdivé? Poznámka: Nejedná se o CBCT jako 3D modalitu s flat panel detektorem, ale o tvar rtg svazku, kdy byl vějířový svazek nahrazen tzv. cone-beam svazkem.
a) Cone-beam svazek je na multidetektorových CT
b) U cone-beam CT platí, že periferní (vnější) detektory zachycují zeslabení z několika sousedních řezů
c) Rekonstrukce u cone-beam je jednodušší než u vějířového svazku
d) Cone-beam svazky jsou polychromatické

Q6: Prepacientská filtrace (mezi rentgenkou a pacientem) u multidetektorového CT:
a) Určuje prostorové rozlišení
b) Redukuje tvrdnutí rtg svazku
c) Zvyšuje tvrdnutí rtg svazku
d) Se používá pro tvarování rtg svazku

Q7: Která data jsou filtrována při zpětné filtrované projekcí?
a) Rekonstruovaná obrazová data
b) Projekovaná data
c) Data lokalizačního skenu
d) Koronální nebo sagitální rekonstruované obrazy

Q8: Kvantový šum u CT lze snížit:
a) Menší tloušťkou řezu
b) Zvýšením mA
c) Větší tloušťkou pacienta
d) Snížením kV

Q9: Multidetektorové CT má celkovou kolimaci 16 mm a pohyb stolu 24 mm/rotace. Jaký je pitch faktor?
a) 0,5
b) 0,7
c) 1,0
d) 1,5

Q10: Posune-li se stůl u helikálního skenu o 18 mm/rotace a pitch faktor je 1,2, jaká je celková kolimace svazku?
a) 2,1 mm
b) 21 mm
c) 1,5 mm
d) 15 mm

Q11: Který z následujících kroků zlepší podezřelost léze (bude zřetelnější, o jakou lézi se jedná)?
a) Snížení matice rekonstruovaného obrazu
b) Zmenšení tloušťky rekonstruovaného řezu
c) Snížení mA
d) Zvýšení šířky okna

Q12: Je-li napětí nastaveno na 100 kV, pak:
a) Všechny emitované fotony mají energii 100 keV
b) Průměrná hodnota energie všech fotonů je 10 keV
c) Průměrná energie všech fotonů, které dopadnou na detektor, je 100 keV
d) Maximální energie emitovaných fotonů je 100 keV

Q13: Má-li materiál lineární součinitel zeslabení menší než voda, pak jeho CT číslo bude:
a) Negativní
b) Pozitivní
c) Nelze říct bez znalosti hustoty materiálu
d) Nelze říct bez znalosti chemického složení

Q14: Která z následujících možností neovlivňuje CT číslo voxelu?
a) Šířka okna
b) kV
c) Zeslabení okolní tkáně
d) Konvoluční kernel (filtr)

Q15: Který z typů detektorů se nejčastěji využívá na CT?
a) Scintilační detektory
b) Plynové detektory
c) Kalorimetry
d) Všechny výše uvedené, záleží na výrobci

Q16: Hrubá (raw) CT data:
a) Obsahují odezvy detektorů pro všechny projekce při akvizici
b) Obsahují rekonstrukční data pro různé tloušťky řezů
c) Jsou typicky mnohem menší než rekonstruované obrazy
d) Vypadají jako rozmazaný obraz pacienta

Q17: Které z následujících CT čísel se zobrazí bílou barvou při šířce okna 400 (WW) a středu okna 60 (WC)?
a) CT čísla nad 60 HU
b) CT čísla v rozsahu -140 až +260 HU
c) CT čísla pod -400 HU
d) CT čísla na +260 HU

Q18: Jaký je objem voxelu CT skenu o tloušťce 3 mm a velikosti pixelu 1 mm?
a) 0,3 mm^3
b) 3 mm^3
c) 30 mm^3
d) 0,3 cm^3

Q19: Jaký je rozdíl mezi pixelem a voxelem?
a) Žádný, pouze jiný název
b) Voxel reprezentuje element v pravidelné 3D síti, pixel reprezentuje element v 2D síti
c) Voxely se používají na MR, zatímco pixely na CT
d) Voxely se používají na CT, zatímco pixely na MR

Q20: Který z následujících parametrů při zachování všech ostatních parametrů konstantních zlepší prostorové rozlišení?
a) Zvýšení pitch faktoru
b) Zvýšení tloušťky řezu
c) Zmenšení velikosti ohniska
d) Zvýšení šířky okna

Q21: Jaké je typické in-plane rozlišení (v rovině XY, tj. kolmé na pacienta, axiální rovina) u CT skenu břicha?
a) 0,01-0,05 mm
b) 0,1-1,0 mm
c) 1-5 mm
d) 10-15 mm

Q22:  Jaké je typické rozlišení v podélné ose pacienta? (osa Z) u CT skenu břicha?
a) 0,01-0,05 mm
b) 0,1-1,0 mm
c) 1-5 mm
d) 10-15 mm

Q23: Který z následujících parametrů při zachování všech ostatních parametrů konstantních sníží dávku pacientovi?
a) Zvětšení velikosti pacienta
b) Zvýšení mA
c) Zvýšení pitch faktoru
d) Zvýšení počtu řad detektorů

Q24: Pro zlepšení prostorového rozlišení při zachování šumu v CT obraze je potřeba:
a) Zmenšit tloušťku řezu a snížit mA
b) Zmenšit tloušťku řezu a zvýšit mA
c) Zmenšit tloušťku řezu a zvětšit matici
d) Zmenšit tloušťku řezu a zvýšit pitch faktor

Q25: Jaké jsou výhody delší doby CT skenu (prodloužení doby rotace rentgenky v gantry) při zachování všech ostatních parametrů konstantních?
a) Lepší časové rozlišení
b) Lepší rozlišení kontrastu
c) Lepší prostorové rozlišení
d) Šetření rentgenky

Q26: Jakým způsobem lze získat z veličiny CTDI_w veličinu CTDI_vol?
a) Vynásobením číslem 1
b) Vynásobením pitch faktorem
c) Vynásobením 1/pitch faktor
d) Vynásobením skenovanou délkou

Q27: Která kombinace následujících parametrů představuje nejvyšší radiační zátěž pro pacienta?
a) 120 kV; 200 mA; 0,5 s doba rotace; 0,8 pitch faktor
b) 120 kV; 150 mA; 1,0 s doba rotace; 1,0 pitch faktor
c) 90 kV; 150 mA; 1,5 s doba rotace; 1,5 pitch faktor
d) 140 kV; 200 mA; 0,5 s doba rotace; 1,5 pitch faktor

Q28: Jak se liší dentální CBCT od klasického CT skeneru?
a) Rotačním časem
b) FOV (field of view)
c) Rozsahem použitelných kV
d) Všechny možnosti

Q29: Jaká je přibližná dávka na plod při CT vyšetření břicha těhotné pacientky (myšleno na jednu fázi)?
a) 0,01-0,05 mGy
b) 0,10-0,50 mGy
c) 1-5 mGy
d) 10-50 mGy

Q30: Jaká je přibližná dávka na kůži při CT vyšetření?
a) 0,03 mGy
b) 0,3 mGy
c) 3 mGy
d) 30 mGy

Odpovědi:
A1: c) Kolimuje rtg svazek dopadající na pacienta
A2: b) Šířkou rtg svazku
A3: c) Šířkou individuálního detektoru a tím, jsou-li informace sousedních detekčních elementů kombinovány
A4: b) Stůl je stacionární, ale rentgenka se kontinuálně pohybuje
A5: c) Rekonstrukce u cone-beam je jednodušší než u vějířového svazku
A6: d) Se používá pro tvarování rtg svazku
A7: b) Projekovaná data
A8: b) Zvýšením mA
A9: b) 1,5 (posun stolu/celková kolimace)
A10: d) 15 mm
A11: b) Zmenšení tloušťky rekonstruovaného řezu
A12: d) Maximální energie emitovaných fotonů je 100 keV
A13: a) Negativní
A14: a) Šířka okna
A15: a) Scintilační detektory
A16: a) Obsahují odezvy detektorů pro všechny projekce při akvizici
A17: d) CT čísla na +260 HU
A18: b) 3 mm^3
A19: b) Voxel reprezentuje element v pravidelné 3D síti, pixel reprezentuje element v 2D síti
A20: c) Zmenšení velikosti ohniska
A21: b) 0,1-1,0 mm
A22: c) 1-5 mm
A23: c) Zvýšení pitch faktoru
A24: b) Zmenšit tloušťku řezu a zvýšit mA
A25: d) Šetření rentgenky
A26: c) Vynásobením 1/pitch faktor
A27: b) 120 kV; 150 mA; 1,0 s doba rotace; 1,0 pitch faktor (závislost je kV^2*mAs*1/pitch)
A28: d) Všechny možnosti
A29: d) 10-50 mGy
A30: d) 30 mGy

Rtg vyšetření srdce a plic (3)

Napsat komentář

V předešlých příspěvcích jsme si řekli o PA projekci vestoje (standardně prováděná na stacionárním skiagrafickém systému) a AP projekci vleže (nejčastěji prováděná na pojízdném skiagrafickém systému na lůžku) a o jejich výhodách. Mimo tyto dvě často zmiňované projekce je možné při rtg vyšetření srdce a plic provést také bočnou neboli laterální projekci. Obě projekce jsou i s velmi užitečným popisem jednotlivých struktur uvedeny na obr. 1.

Obr. 1: PA a laterální projekce při rtg srdce a plic (Normal, Labelled, Chest x-ray – Undergraduate Diagnostic Imaging Fundamentals (pressbooks.com))

Při laterální projekci stojí pacient levým bokem k receptoru obrazu, takže rtg svazek vstupuje do jeho pravého boku a vystupuje z pacientova levého boku. Důvodem je zde opět anatomická stavba pacienta – srdce je umístěno více vlevo, takže při této pozici dělá srdce menší srdeční stín. Laterální projekce je prováděna často jako doplňující vyšetření k PA projekci.

Při PA a laterální projekci u vertigrafu musí být pacient schopen stát nebo sedět ve vzpřímené pozici, měl by být schopen zadržet dech a v neposlední řadě by měl být schopen spolupracovat. Rtg svazek vstupuje do zad pacienta a poté vystupuje na přední straně pacienta.

AP projekce vleže se provádí u těch pacientů, u kterých není možné provést PA projekci u vertigrafu (vestoje ani vsedě). Většinou se jedná o pacienty ve vážném stavu. Receptor obrazu, dnes nejčastěji flat panel detektor, případně CR kazeta, se vkládají pod pacienta, rentgenka je umístěna nad pacientem. Rtg svazek vstupuje do pacienta zepředu a vystupuje ze zad. Ukázka rtg obrazu stejného pacienta získaná při PA projekci vestoje a následně v AP projekci na lůžku je uvedena na obr. 2.

Obr. 2: PA projekce vestoje a AP projekce vleže

Dalším typem projekce je lordotická projekce. Lordotická projekce je taková projekce na plíce, u které rtg svazek vstupuje do pacienta zepředu a prochází šikmo vzhůru (buď je nastaven rtg svazek tímto směrem nebo je šikmo umístěn pacient a rtg svazek směřuje horizontálně). Rtg obraz se od standardního PA obrazu odlišuje v tom, že klíční kosti nepřekrývají plíce, konkrétně tedy plicní hroty (apexy). Ukázka pozice rentgenky a detektoru a rtg obrazu při PA a lordotické projekci jsou uvedeny na obr. 3. Tato projekce je dnes prováděna velmi zřídka.

Obr. 3: Lordotická projekce – pozice rentgenky a detektoru (A), rtg obraz v PA projekci (B) a rtg obraz v lordotické projekci (C) (Imaging Techniques | Thoracic Key)

Velmi detailní anatomický popis a objasnění projekcí při rtg vyšetření srdce a plic je také v následujícím videu: Chest X-ray: Introduction and Approach – YouTube. Vřele doporučuji.

To je již vše o rtg vyšetření srdce a plic. Je to psáno z pohledu fyzikálního, proto se občas mohou vyskytnout nějaké anatomické nepřesnosti, za které se omlouvám.

Použitá literatura
Types of X-Ray examinations – YouTube
Normal, Labelled, Chest x-ray – Undergraduate Diagnostic Imaging Fundamentals (pressbooks.com)
Imaging Techniques | Thoracic Key

Rtg vyšetření srdce a plic (2)

Napsat komentář

V předešlém příspěvku jsme si řekli již o některých výhodách zadopřední (PA) a předozadní (AP) projekce, přičemž PA se používá při pozici pacienta u vertigrafu, AP pak u pacientů vyšetřovaných na lůžku.

Jednou z nevýhod AP geometrie při vyšetření na lůžku je zvětšení obrazu. Asi by nám obecně nepřišlo špatné, vidět patologii zvětšenou, ale problém nastává proto, že v rtg obraze je zvětšeno pouze něco. Právě orgány vzdálenější od receptoru obrazu jsou více zvětšené než orgány nacházející se blízko receptoru obrazu, dochází tam k falešnému zvětšení. Několik grafických znázornění, jak dochází k onomu zvětšení, je uvedeno na následujících obrázcích.

Na obr. 1 je uveden vliv vzdálenosti ohniska (na obr. 1 označen „X-ray source“) od vyšetřovaného objektu při zachování vzdálenosti vyšetřovaný objekt – receptor obrazu.

Obr. 1. Vliv vzdálenosti ohniska od vyšetřovaného objektu na zvětšení rtg obrazu při zachování konstantní vzdálenosti vyšetřovaný objekt – receptor obrazu [Imaging the Chest: The Chest Radiograph | Radiology Key]

Z obr. 1 je zřejmé, že čím větší vzdálenost ohnisko – vyšetřovaný objekt, tím je zvětšení rtg obrazu menší, tedy velikost rtg obrazu více odpovídá reálné velikosti.

Na obr. 2 je uveden vliv vzdálenosti vyšetřovaného objektu od receptoru obrazu při zachování vzdálenosti ohnisko – vyšetřovaný objekt. Jde tedy pouze o oddálení receptoru obrazu od vyšetřovaného objektu.

Obr. 2: Vliv vzdálenosti receptoru obrazu od vyšetřovaného objektu na zvětšení rtg obrazu při zachování konstantní vzdálenosti ohnisko – vyšetřovaný objekt [Imaging the Chest: The Chest Radiograph | Radiology Key]

Z obr. 2 je zřejmé, že čím menší vzdálenost receptor obrazu – vyšetřovaný objekt, tím je zvětšení rtg obrazu menší, tedy velikost rtg obrazu více odpovídá reálné velikosti.

Nyní spojíme všechny výše uvedené skutečnosti do praktického provedení rtg vyšetření srdce a plic: PA projekce s velkou ohniskovou vzdáleností (vzdálenost ohnisko – receptor obrazu 180-200 cm) a AP projekce s malou ohniskovou vzdáleností (vzdálenost ohnisko – receptor obrazu 80-100 cm). Grafické znázornění je uvedeno na obr. 3.

Obr. 3: Vliv PA a PA projekce na zvětšení rtg obrazu [Imaging the Chest: The Chest Radiograph | Radiology Key]

Při pohledu na obr. 3 je zřejmé, že při AP projekci dostáváme zvětšený rtg obraz, ale srdce je v něm zvětšeno více ve srovnání se zvětšením samotného hrudníku než při PA projekci. Právě na to je nutné pamatovat při popisu rtg vyšetření provedených na lůžku. Ukázka rtg obrazu stejného pacienta získaná v krátké době po sobě v PA projekci vestoje a AP projekci vleže je uvedena na obr. 4. Obr. 4 vlevo by mohl být lépe zobrazen použitím widowingu a levellingu.

Obr. 4: Rtg obraz srdce a plic pořízený v PA projekci u vertigrafu a AP projekci na lůžku [Imaging the Chest: The Chest Radiograph | Radiology Key]

Z obr. 4 je zřejmé, že při PA projekci vestoje je srdeční stín menší, současně implantovaný kardiostimulátor/defibrilátor vypadá menší, resp. více odpovídá reálné velikosti. Při PA projekci vestoje je možné zajistit kolmost rtg svazku na tělo pacienta a současně kolmost rtg svazku na receptor obrazu, zatímco u AP projekce na lůžku není kolmost často splněna. Při PA projekci vestoje je bránice posunuta níže, jsou zobrazeny expandované plíce, zatímco při AP projekci vleže může být spodní část plic zastíněna. Podobně s výpotkem na plicích. Při PA projekci vestoje bude tekutina umístěna v dolní části plic, zatímco při pozici vleže bude tekutina na více místech, případně bude rozprostřená po celých plicích, což se projeví vyšší denzitou celých plic a nemusí být v rtg obraze tak jasně viditelná jako při projekci vestoje. Při PA projekci vestoje má pacient přitisknuté všechny struktury na vertigraf stejně (horní a dolní část hrudníku), zatímco u AP projekce na lůžku se více projev lordotická pozice – různá vzdálenost horní a dolní části hrudníku od rentgenky. Přehled dalších možných patologií, které se mohou v rtg obraze projevit právě kvůli AP projekci na lůžku jsou uvedeny v tab. 1.

Tab. 1: Patologie vznikající v rtg obrazu v důsledku AP projekce na lůžku [Imaging the Chest: The Chest Radiograph | Radiology Key]

Při AP projekci na lůžku dochází častěji k rotaci těla, takže hrudník není zobrazen v rtg obraze symetricky, viz obr. 5, na kterém jsou znázorněny objekty simulující klíční kosti a srdce. Lze to poznat např. podle nesymetrické pozice klíčních kostí, viz obr. 6.

Obr. 5: Simulace klíčních kostí a srdce ve správné a rotované projekci [Imaging the Chest: The Chest Radiograph | Radiology Key]

Obr. 6: Rotovaný rtg obraz pořízení v AP projekci na lůžku [Imaging the Chest: The Chest Radiograph | Radiology Key]

Rtg vyšetření srdce a plic se standardně provádí v nádechu. Avšak jsou pacienti, kteří se nadechnout nedokáží. To se samozřejmě projeví i v rtg obraze. Ukázky rtg vyšetření v nádechu a výdechu jsou zobrazeny na obr. 7.

Obr. 7: Rtg vyšetření v nádechu (vlevo) a ve výdechu (vpravo) [Types of X-Ray examinations – YouTube]

To je pro tentokrát vše, o rtg vyšetření hrudníku bylo něco uvedeno již velmi dávno, v tomto příspěvku. Příště si řekneme ještě něco více k jednotlivým projekcím při rtg vyšetření srdce a plic.

Použitá literatura
Imaging the Chest: The Chest Radiograph | Radiology Key
Types of X-Ray examinations – YouTube

Rtg vyšetření srdce a plic (1)

Napsat komentář

Lékaři popisující rtg snímek srdce a plic by měli být seznámeni s tím, jak se změní vzhled rtg obrazu tehdy, změní-li se geometrie vyšetření. Např. se neprovede zadopřední (PA) ale předozadní (AP) projekce. V dnešním příspěvku si řekneme více o tom, jak se daná geometrie projeví v rtg obraze. Asi to není téma úplně typické pro radiologické fyziky, ale určitě je fajn dozvědět se něco nového a předpokládám, že to může být zajímavé i pro radiologické asistenty, kteří právě taková vyšetření standardně provádějí.

Obecně se dá říct, že je-li to možné, pak při rtg vyšetření srdce a plic stojí pacient u vertigrafu (receptor obrazu svisle umístěný v držáku) na rtg vyšetřovně, což s sebou nese několik výhod, které budou uvedeny postupně. Není-li to možné, pak může např. sedět u vertigrafu na vyšeřovně a není-li ani to možné, pak pacient leží na lůžku, nejčastěji přímo na pacientském pokoji. Jestliže se dokáže pacient posadit, pak je výhodné převézt pacienta i s postelí k vertigrafu a posadit ho na lůžku u vertigrafu. Rtg vyšetření u vertigrafu (vestoje, případně vsedě) je vždy kvalitnější než vleže, už kvůli použití protirozpylové mřížky, ale jsou zde i další geometrické a anatomické důvody.

Při pozici vestoje u vertigrafu se provádí PA projekce, pacient stojí zády k rentgence a čelem k receptoru obrazu. Tedy rtg svazek vstupuje do pacienta zezadu a vystupuje zepředu, poté dopadá na receptor obrazu. U vyšetření na lůžku je to naopak, vyšetření se provádí v AP projekci, rtg svazek vstupuje do pacienta vpředu a vystupuje ze zad, pod kterými je umístěn receptor obrazu. Ukázka PA a AP projekce u vertigrafu je uvedena na obr. 1.

Obr. 1: PA a AP projekce [Imaging the Chest: The Chest Radiograph | Radiology Key]

Důvodem, proč je rtg vyšetření vestoje kvalitnější, je vhodnější anatomická geometrie (srdce blíže receptoru obrazu) a taktéž geometrie akvizice rtg vyšetření (větší vzdálenost mezi ohniskem a pacientem).

Výhoda anatomické geometrie: Srdce je v lidském těle umístěno blíže k přední straně hrudníku (lze vidět i na obr. 1, kde je srdce simulováno šedým oválem v hrudníku). Je-li pacient vyšetřován v PA projekci, pak srdce samotné leží blíže k receptoru obrazu (obr. 1 vpravo), zvětšení je pouze malé a srdce dělá pouze malý srdeční stín. Je-li pacient vyšetřován v AP projekci (obr. 1 vlevo), srdce je od receptoru obrazu dále, takže pak i zvětšení je větší. Názorná ukázka zvětšení je uvedena na obr. 2. Z výše uvedeného vyplývá, že pro získání co nejreálnější velikosti objektu je potřebné umístit ho co nejblíže receptoru obrazu. Z obr. 2 je podle intenzity barvy na receptoru obrazu zřejmé, že je-li vyšetřovaný objekt blíže receptoru obrazu (ruka blíže plátnu), pak je i intenzita v rtg obraze vyšší, neboli části umístěné blíže receptoru obrazu jsou kontrastnější než ty části, které jsou umístěny od receptoru obrazu dále.

Obr. 2: Zvětšení při AP (nahoře) a PA (dole) projekci [Imaging the Chest: The Chest Radiograph | Radiology Key]

Výhoda geometrie akvizice: Je-li pacient vyšetřován u vertigrafu, pak se nejčastěji používá vzdálenost ohnisko – receptor obrazu 180-200 cm. Při rtg vyšetření na lůžku se používá vzdálenost ohnisko – receptor obrazu 80-100 cm. Z toho vyplývá, že rtg obraz na lůžku má větší zvětšení než rtg obraz u vertigrafu, typicky se to týká srdečního stínu. Ukázka výhody geometrie PA vs. AP je uvedena na obr. 3. Z výše uvedeného vyplývá, že pro získání co nejreálnější velikosti objektu je potřebné umístit zdroj záření co nejdále od vyšetřovaného objektu. Dalším nezanedbatelným efektem větší vzdálenosti ohniska od vyšetřovaného objektu je zlepšení geometrické neostrosti způsobené nenulovou velikostí ohniska, ale o tom si řekneme více v následujícím příspěvku.

Obr. 3: Zvětšení vyšetřovaného objektu při malé (nahoře) a velké (dole) ohniskové vzdálenosti [Imaging the Chest: The Chest Radiograph | Radiology Key]

Typicky se při vyšetření na lůžku nepoužívá fyzická protirozptylová mřížka, avšak je možné použít virtuální (softwarovou) mřížku. Nepřítomnost protirozptylové mřížky vede k horší kvalitě rtg obrazu.

Nemá-li popisující radiolog informaci o projekci, může se stát, že podle velikosti srdečního stínu popíše kardiomegalii, ačkoliv jí pacient reálně netrpí.

Poznámka: Kardiomegalie neboli zvětšení srdce, je definována tak, že srdce, resp. srdeční stín, je větší než 0,5x průměr hrudníku. Ukázka měření je uvedena na obr. 4.

Obr. 4: Ukázka měření rozměrů pro stanovení kardiomegalie [How to measure Cardiomegaly in CXR – YouTube]

Postup měření je následující: Nakreslete svislou čáru přes střed těla (páteř). Změřte největší rozměr srdce od svislé čáry vpravo a vlevo. Poté změřte průměr celého hrudníku. Je-li podíl šířky srdečního stínu (A+B) větší než 0,5*C (šířka hrudníku), pak se jedná o kardiomegalii. Poměr (A+B)/C se nazývá také kardiotorakální index – poměr šířky srdečního stínu/šířky hrudníku.

Více o výhodách a nevýhodách PA a AP projekce při rtg vyšetření srdce a plic si řekneme v následujícím příspěvku.

Použitá literatura
Imaging the Chest: The Chest Radiograph | Radiology Key
How to measure Cardiomegaly in CXR – YouTube
Microsoft PowerPoint – Guidelines SS, diagnostika SS.ppt [režim kompatibility] (kardio-cz.cz)

Kumulativní efektivní dávky z opakovaných radiodiagnostických vyšetření

Napsat komentář

V posledních letech jsou dost ožehavým tématem dávky z opakovaných radiodiagnostických vyšetření. V tomto případě není opakovanými vyšetřeními myšleno znovuprovedení vyšetření z důvodu např. špatné kvality obrazu, ale situace, kdy pacienti podstupují některá vyšetření opakovaně z důvodu sledování léčby. Touto tématikou se zabýval také virtuální meeting ve dnech 19.-23. 10. 2020 uspořádaný International Atomic Energy Agency. Alespoň některé postřehy bych tu ráda uvedla, ale pro začátek uvedení do problematiky.

Různé studie ohledně kumulativních dávek z opakovaných vyšetření, zejména CT vyšetření, se začaly objevovat už cca před 10 lety, avšak pouze velmi výjimečně. Odhady kumulativních dávek v těchto studiích byly většinou založeny na vynásobení typických dávek počtem vyšetření. Mimo to se objevilo i několik studií, které se zabývaly kumulativními dávkami pro specifická onemocnění, zejména ta, u kterých pacienty často podstupují radiodiagnostické výkony. Typicky se jedná o pacienty s Crohnovou chorobou, s kardiologickým onemocněním, selhávajícími ledvinami, implantovanými stentgrafty atd.

Studie zabývající se kumulativními efektivními dávkami se ve větší míře objevují i dnes, avšak s podstatně přesnějšími odhady kumulativních efektivních dávek. Odhady kumulativních efektivních dávek jsou založeny na dose management softwarech neboli softwarech pro sledování dávek (více např. v příspěvku o CT optimalizaci). Díky těmto softwarům je již možné podstatně jednodušším způsobem určit, která onemocnění jsou spojena s vyššími kumulativními dávkami a také jaké přibližně jsou tyto kumulativní dávky. Do popředí zájmu se pak dostávají pacienti, u nichž je kumulativní efektivní dávka vyšší než 100 mSv.

Dříve se žilo v domnění, že pacienti s kumulativními efektivními dávkami vyššími než 100 mSv jsou spíše pacienti léčení ve speciálních centrech a že jsou to převážně starší pacienti s maligním onemocněním nebo s onemocněním s velmi špatnou prognózou. Takže se této problematice nevěnovala příliš pozornost.

Nové světlo na tuto problematiku vrhly až nedávno publikované studie, za nimiž často stál Madan Rehani, který se v poslední době zabývá osvětou této problematiky. Studie zahrnující CT vyšetření byly provedeny ve spolupráci s různými státy a zdravotnickými zařízeními. Mezi tyto studie patří zejména tři následující:

Zde jsou odkazy ke stažení jednotlivých článků:
Patients undergoing recurrent CT scans: assessing the magnitude (Rehani, M.)
Patients undergoing recurrent CT exams: assessment of patients with non-malignant diseases, reasons for imaging and imaging appropriateness (Rehani, M.)
Multinational data on cumulative radiation exposure of patients from recurrent radiological procedures: call for action (Brambilla, M.)

Do studií bylo zahrnuto 344 nemocnic ze 20 zemí, využívající 344 CT skenerů. Sběr dat trval od 1 do 5 let. Zahrnuto bylo 3,3 mil. pacientů (pouze ti, kteří podstoupili CT vyšetření opakovaně, ostatní pacienti zahrnuti nebyli), kteří podstoupili přes 5 mil. CT vyšetření. Ve studiích se řešil počet pacientů, kteří obdrží kumulativní efektivní dávku (CED, cumulative effective dose) vyšší než 100 mSv. Jen pro upřesnění proč zrovna mezní hodnota 100 mSv. Efektivní dávka 100 mSv bývá často označována jako hranice mezi „nízkými“ a „vysokými“ dávkami, u dávek nad 100 mSv byla ve studiích statisticky prokázána vyšší pravděpodobnost vzniku stochastických účinků.

Ze studií vyplynulo, že kumulativní dávku vyšší než 100 mSv obdrží 1,5 % pacientů, pro různé nemocnice se tato hodnota pohybovala mezi 0,6-3,4 % pacientů. V průměru se dá říct, že každý stý pacient obdrží kumulativní dávku z CT vyšetření vyšší než 100 mSv. Maximální počet CT vyšetření na jednoho pacienta byl 109 CT vyšetření, což mi popravdě přijde neuvěřitelné…

Následně Madan Rehani publikoval další článek (viz níže), ve kterém uvádí, že ve 35 zemích OECD se dá předpokládat, že přibližně 2,5 mil. pacientů obdrží kumulativní efektivní dávku vyšší než 100 mSv v průběhu pěti let.

V tomto naposled zmiňovaném článku se objevil odhad počtu pacientů s kumulativní efektivní dávkou vyšší než 100 mSv pro různé země (viz obr. 1), včetně České republiky. V České republice obdrží pravděpodobně 1 pacient na 1 tis. obyvatel kumulativní efektivní dávku vyšší než 100 mSv za pět let. Při počtu 10,5 mil. obyvatel to znamená, že za oněch pět let máme v ČR přibližně 10,5 tis. pacientů s kumulativní efektivní dávkou vyšší než 100 mSv. Což není úplně málo. Další šokující zjištění na základě analýzy dat přišlo následně, když se zjistilo, že více než 1 tis. pacientů obdržel za jeden den kumulativní efektivní dávku vyšší než 100 mSv a 31 tis. pacientů obdrželo kumulativní efektivní dávku vyšší než 50 mSv za jeden den. To znamená, že tito pacienti podstoupili i několik CT vyšetření během jednoho dne (navíc zde nejsou zahrnuty ještě další radiodiagnostické, případně radioterapeutické výkony, např. intervenční výkony, u který pacienti také mohou v jednom sezení obdržet několik desítek mSv). Často se vůbec nejednalo o starší pacienty, 20 % pacientů bylo mladší než 50 let, tj. každý pátý pacient. Z hlediska indikací, a tedy onemocnění, se ukázalo, že 10 % pacientů bylo indikováno k CT vyšetření z důvodu nemaligního onemocnění.

Obr. 1: Počet pacientů s kumulativní efektivní dávkou vyšší než 100 mSv za 5 let normovaný na 1000 obyvatel

Použitá literatura
Rehani, M. Radiation doses in recurrent imaging: Where do we stand and way forward? Technical meeting on the justification and optimization of protection of patients requiring multiple imaging procedures. IAEA, October 19-23, 2020

Jaká je role klinického radiologického fyzika?

Napsat komentář

V tomto příspěvku bych ráda řekla něco více o tom, jaká je a kam směřuje role klinického radiologického fyzika (KRF) v radiodiagnostice a intervenční radiologii. Budu při tom vycházet z nově vydané knihy Clinical Imaging Physics. Current and emerging practice, která se mi nedávno dostala do rukou. Hlavním editorem byl profesor Ehsan Samei, takže už toto jméno samo o sobě říká, že knížka bude zajímavá a na dobré úrovni.

Když se vrátíme o dekádu zpět, tak hlavním úkolem KRF v radiodiagnostice bylo testování rtg systémů, tj. primárně šlo o provádění zkoušek dlouhodobé stability a zkoušek provozní stálosti (přístup k testování se pro každé pracoviště liší, někde byly a jsou zkoušky prováděny externími subdodavateli), a případně také stanovení diagnostických referenčních úrovní. V posledních letech k tomu přibylo také provedení externích klinických auditů. Nicméně ta jeho hlavní role v dnešní době se posouvá více do klinické části a o tom si právě dnes řekneme.

Na začátku si vypůjčím hned první tabulku z citované publikace, viz obr. 1. V tabulce je skvěle shrnuto, co se očekává od KRF. Ačkoliv je to myšleno obecně, pod tabulkou je pak volný překlad a objasnění, co je tím myšleno primárně v radiodiagnostice a intervenční radiologii.

Obr. 1: Očekávání a klíčové činnosti klinického radiologického fyzika [1]

  • Ad 1) „Vědec v místnosti“: KRF je člověk, který by ze své podstaty měl mít vědecké myšlení a porozumět tzv. evidence-based přístupu. Tedy dokáže analyzovat závěry plynoucí z různých publikací, porozumět limitacím a poznatky technicky převést do klinické praxe v konkrétních situacích.
  • Ad 2) Zajištění kvality a bezpečnosti: KRF by měl v klinické praxi zajistit požadovanou kvalitu, přesnost a bezpečnost napříč všemi zobrazovacími systémy. Existuje nepřeberné množství zobrazovacích systémů a z neznalosti a neoptimálního nastavení některých těchto systémů mohou vznikat chyby v diagnostice. KRF by měl být schopen zajistit, aby každý systém poskytoval to, co od něho klinik, který na něm pracuje, očekává, z hlediska kvality obrazu a bezpečnosti, aby se tak co nejvíce zamezilo možným chybám.
  • Ad 3) Splnění požadavků regulátorů: KRF by měl zajistit, že rtg systémy a praxe při provádění různých výkonů bude splňovat požadavky kladené regulátory, např. soulad s atomovým zákonem a příslušnými vyhláškami. Od KRF se očekává velmi aktivní přístup při aplikaci nových poznatků (měl by být inovátor), protože legislativa je většinou o krok pozadu a není tedy možné očekávat, že se nové techniky objeví tak rychle v různých dokumentech a doporučeních.
  • Ad 4) Relevantní hodnocení technologie: KRF by měl být schopen zhodnotit, zda daná zobrazovací technologie umožňuje dosažení požadovaného výsledku, a to zejména v kontextu prováděných testů a měření (QC), avšak uzpůsobit tato měření na hodnocení celkového výstupu ze systému neboli přejít od compliance-based (dodržení toho, co tvrdí výrobce a co je dáno legislativou) k performance-base hodnocení.
  • Ad 5) Optimalizace: Jedna z velmi podstatných činností, kterou by měl provádět KRF v týmu společně s radiologem, radiologickým asistentem a případně také aplikačním technikem. Každému pracovišti vyhovuje jiný přístup, proto obecné nastavení od výrobce nemusí být vždy ideální a je potřeba přizpůsobit zobrazovací techniku potřebám daného pracoviště. Jedná se o nastavení zobrazovacího řetězce, zejména z hlediska kvality obrazu (včetně postprocessingu) a dávky tak, aby systém skutečně poskytoval maximum z toho co umí, nikoliv aby se stalo, že systém v rámci různých testů a měření prokáže skvělé charakteristiky, které se však v klinické praxi pak neuplatní.
  • Ad 6) Sledování (monitorování) situace: Tím je zde myšlena retrospektivní analýza aktuálního přístupu nejen z hlediska optimalizace, ale i z hlediska kvality a bezpečnosti celého zobrazovacího řetězce a případných komplikací vznikajících z jiných důvodů než neoptimálního nastavení techniky.
  • Ad 7) Pořízení nové technologie: KRF by měl umět zanalyzovat výhody a nevýhody různých zobrazovacích systémů a to nejen obecně, ale také z hlediska výkonů a potřeb jednotlivých pracovišť, aby pak nově pořízené zobrazovací systémy vyhovovali požadavkům kliniků, tj. aby byly ušity na míru daných pracovišť. S tím souvisí zavádění nových technik, např. v dřívější době zavedení přímé digitalizace, cone-beam CT, pokročilejší rekonstrukce atd.
  • Ad 8) Převzetí technologie: Tímto bodem je myšlen správný postup při zavádění nového systému do klinické praxe. Např. při zakoupení nového zobrazovacího systému by měl být KRF nápomocen z hlediska technických znalostí radiologovi a radiologickému asistentovi, aby se správně nastavil přístup k použití nového systému.
  • Ad 9) Spolupráce s výrobcem: To je bod, který bohužel není příliš relevantní v České republice. K výrobci se téměř nikdo z nás nedostane a maximum, co pro nás mohou čeští zástupci výrobců udělat je, že předají naše požadavky dále, aby se dostali až k výrobcům a ti je pak případně mohli zhodnotit a zkusit aplikovat při dalším vývoji. Každý výrobce má různě po světě několik svých referenčních pracovišť, kde probíhá testování zobrazovacích systémů v praxi a jejich další modifikace, ale obecně v České republice až na výjimky spolupráce s výrobci příliš nerozkvétá.
  • Ad 10) Posun v praxi: KRF by měl být nápomocen při zlepšování klinické praxe, aby dokázal zanalyzovat a v klinické praxi uplatnit nové poznatky, a tím tu praxi posunout dále.
  • Ad 11) Konzultant pro výzkum: KRF by měl být schopen poskytnout relevantní publikace a rady v různých vědeckých projektech týkajících se zobrazování.
  • Ad 12) Poskytovatel dalšího vzdělání: KRF by měl být schopen dále vzdělávat kliniky, resp. pracovníky pracující se zobrazovacími systémy, z hlediska použití zobrazovací systémů, např. jak systém funguje a jak nefunguje :), ale také z hlediska radiační ochrany a optimalizace.

Ještě bych se vrátila k bodu 1). Každý radiologický fyzik v rámci svého studia získá velmi dobré fyzikální a matematické základy a také analytické myšlení. Na tom je dále stavěna odborná část – dozimetrie, detekce, zobrazovací technika, zpracování obrazu. K tomu se přidávají i znalosti z lékařské oblasti – anatomie, patologie, patofyziologie, radiobiologie… A propojením všech těchto oblastí dohromady by KRF  měl být odborníkem, který dokáže analyzovat různé problémy a navrhnout k nim smysluplné řešení nebo změnu přístupu, např. na základě odborných publikací, který bude vhodnější, bezpečnější, konzistentnější a za přijatelnou cenu (finanční náklady, ale také z hlediska zdravotní újmy). Tohoto bychom měli využívat v naší práci a být tím „mozkem“, který posune klinickou praxi dále (skvěle to popisuje jeden slogan, který jsem nedávno zahlédla v jedné přednášce „Today’s research is tomorrow‘ s practice“), samozřejmě ve spolupráci s lékaři, nejen radiology, radiologickými asistenty, servisními a aplikačními techniky. My, kliničtí radiologičtí fyzici :), bychom měli být ti, co vědí, jak daná technologie funguje, jak ji správně používat a optimalizovat, abychom nezpůsobili více škody než užitku. Některé z výše uvedených bodů bohužel nemohou splnit externí radiologičtí fyzici, protože se jedou na pracoviště pouze občas podívat, tak doufejme, že v budoucnu bude stále více těch, kteří opravdu jsou v té jedné nemocnici a snaží se splnit to, co se od nich očekává ;).

Použitá literatura
[1] Samei E, Pfeiffer DE. Clinical imaging physics. Current and emerging practice. Wiley Blackwell 2020; ISBN 9781118753453